Decomposição (SVD e PCA)
Resumo de SVD e entendimento de PCA. Necessita de uma base em álgebra linear.
Resultados Esperados
- Entender SVD no escopo de ciência de dados
- Entender PCA no escopo de ciência de dados
- Saber fazer uso dos dois (interpretar componentes e fatores)
Sumário
#In:
from scipy import stats as ss
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#In:
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.axisbelow'] = True
plt.rcParams['axes.grid'] = True
plt.rcParams['axes.labelsize'] = 16
plt.rcParams['axes.linewidth'] = 2
plt.rcParams['axes.spines.bottom'] = True
plt.rcParams['axes.spines.left'] = True
plt.rcParams['axes.titlesize'] = 16
plt.rcParams['axes.ymargin'] = 0.1
plt.rcParams['font.family'] = 'serif'
plt.rcParams['grid.color'] = 'lightgrey'
plt.rcParams['grid.linewidth'] = .1
plt.rcParams['xtick.bottom'] = True
plt.rcParams['xtick.direction'] = 'out'
plt.rcParams['xtick.labelsize'] = 16
plt.rcParams['xtick.major.size'] = 12
plt.rcParams['xtick.major.width'] = 1
plt.rcParams['xtick.minor.size'] = 6
plt.rcParams['xtick.minor.width'] = 1
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'out'
plt.rcParams['ytick.labelsize'] = 16
plt.rcParams['ytick.left'] = True
plt.rcParams['ytick.major.size'] = 12
plt.rcParams['ytick.major.width'] = 1
plt.rcParams['ytick.minor.size'] = 6
plt.rcParams['ytick.minor.width'] = 1
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams['legend.fontsize'] = 16
plt.rcParams['lines.linewidth'] = 4
plt.rcParams['lines.markersize'] = 80
#In:
plt.style.use('tableau-colorblind10')
plt.ion();
Introdução
Na álgebra linear, a decomposição em valores singulares ou singular value decomposition (SVD) é a fatoração de uma matriz real ou complexa, com diversas aplicações importantes em processamento de sinais e estatística.
Formalmente, a decomposição em valores singulares de uma matriz m×n real ou complexa X é uma fatoração ou fatorização na forma:
\[X = U \Sigma V^{*}\]Aqui, $U$ é a matriz de vetores singulares à direita. $\Sigma$ é uma matriz diagonal com os valores singulares. Por fim, $V^{}$ é a transposta conjugada dos valores singulares à direita. *Possivelmente você deve estar pensando: “massa, um monte de termo que sei muito pouco sobre”. Se este é o seu caso, não se preocupe! Vamos tentar focar em uma ideia mais simples, que faria um matemático chorar, para explicar SVD.
Para tal, uma outra forma de escrever tal equação é:
\[X = U_s V^{t}\]onde, $U_s = U \Sigma$, ou seja, o produto da primeira parte da equação acima. Aqui, $V^{t}$ é simplesmente transposta de $V$. Não vamos nos preocupar com transpostas conjugadas pois vamos trabalhar com números reais.
Em sua forma correta, $ X = U \Sigma V^{*} $, SVD consegue decompor qualquer matriz, $X$, real ou complexa. A decomposição também vai ser complexa, isto é, $U$, $\Sigma$ e $V$ podem conter números complexos. É importante ressaltar este fato para deixar claro que SVD consegue trabalhar no espectrograma complexo caso seja necessário. Fazemos uso da versão modificada aqui, pois conseguimos visualizar o espectro usando a norma dos números complexos, ou seja, um valor real.
Como entender SVD melhor?
Começando com vetores
Vamos voltar para a nossa simplificação acima: $ X = U_s V^{t} $. Agora, vamos definir $U_s$ como um vetor coluna, i.e.,:
\begin{align} U_s &= \begin{bmatrix} c_{1}
c_{2}
\vdots
c_{n} \end{bmatrix} \end{align}
Além do mais, vamos também definir $V$ como um outro vetor coluna. Como trabalhamos com $V^t$, teremos a transposta, ou seja, um vetor linha na nossa expressão de SVD. Segue a forma de $V^t$.
\begin{align} V^t &= \begin{bmatrix} l_{1}, l_{2}, \cdots, l_{m} \end{bmatrix} \end{align}
A nossa expressão então vira:
\begin{align} X &= \begin{bmatrix} c_{1}
c_{2}
\vdots
c_{n} \end{bmatrix}\begin{bmatrix} l_{1}, l_{2}, \cdots, l_{m} \end{bmatrix} \end{align}
Observe como o produto de um vetor coluna de tamanho $(n, 1)$ com um outro linha de tamanho $(1, m)$ gera uma matriz de tamanho $(n, m)$. Agora, uma coisa importante deste produto é que o mesmo tem posto matricial igual à um. O que isto quer dizer? Que toda linha ou coluna da matriz resultante é, de certa forma, redundante. Pois as outras são uma combinação linear da mesma. Para entender isto observe o produto abaixo.

Observe como todas as linhas da matriz acima são da forma: $c_i \cdot [ l_1 \cdots l_m]$. Aqui, $i$ é a linha. Desta forma, todas as linhas tem como base o vetor $ [ l_1 \cdots l_m] $, porém, escalados por uma constante diferente $c_i$.
Observe que a escolha de transformar: $U_s$ e $V$ em vetores colunas foi bem arbitrária. Podemos usar outros tamanhos.
Aumentando a dimensão um pouco
Agora, vamos definir $U_s$ como uma matriz com DUAS colunas, i.e.,:
\begin{align} U_s &= \begin{bmatrix} c_{1,1},\,\, c_{1,2}
c_{2,1},\,\, c_{2,2}
\vdots
c_{n,1},\,\, c_{n,2} \end{bmatrix} \end{align}
Similarmente, segue a nova forma de $V^t$.
\begin{align} V^t &= \begin{bmatrix} l_{1, 1}, \,\, l_{1, 2}, \,\, \cdots, \,\, l_{1, m}
l_{2, 1}, \,\, l_{2, 2}, \,\, \cdots , \,\, l_{2, m}
\end{bmatrix} \end{align}
Observe como será
\begin{align} X = \begin{bmatrix} c_{1,1}l_{1,1} + c_{1,2}l_{2,1} ,\,\,\,\, c_{1,1}l_{1,2} + c_{1,2}l_{2,2} , \,\,\cdots, \,\,\,\, c_{1,1}l_{1,m} + c_{1,2}l_{2,m}
c_{2,1}l_{1,1} + c_{2,2}l_{2,1} ,\,\,\,\, c_{2,1}l_{1,2} + c_{2,2}l_{2,2} , \,\,\cdots, \,\,\,\, c_{2,1}l_{1,m} + c_{2,2}l_{2,m}
\cdots
c_{n,1}l_{1,1} + c_{n,2}l_{2,1} ,\,\,\,\, c_{n,1}l_{1,2} + c_{n,2}l_{2,2} , \,\,\cdots, \,\,\,\, c_{n,1}l_{1,m} + c_{n,2}l_{2,m} \end{bmatrix} \end{align}
Agora, eu sei que a expressão acima está BEM densa. Mas foque apenas na primeira linha:
\[[ c_{1,1}l_{1,1} + c_{1,2}l_{2,1} ,\,\,\,\, c_{1,1}l_{1,2} + c_{1,2}l_{2,2} , \,\,\cdots, \,\,\,\, c_{1,1}l_{1,m} + c_{1,2}l_{2,m} ]\]Atente para o fato de que o vetor:
\[[ c_{1,1}l_{1,1} ,\,\,\,\, c_{1,1}l_{1,2} , \,\,\cdots, \,\,\,\, c_{1,1}l_{1,m} ]\]É o mesmo resultado que tinhamos antes quando consideramos apenas uma dimensão. O mesmo está sendo somado do vetor:
\[[ c_{1,2}l_{2,1} ,\,\,\,\, c_{1,2}l_{2,2} , \,\,\cdots, \,\,\,\, c_{1,2}l_{2,m} ]\]Qual o motivo disto ser interessante? Podemos re-escrever o produto matricial acima como sendo:
\begin{align} X &= \begin{bmatrix} c_{1, 1}
c_{2, 1}
\vdots
c_{n, 1} \end{bmatrix}\begin{bmatrix} l_{1, 1}, l_{1, 2}, \cdots, l_{1, m} \end{bmatrix} + \begin{bmatrix} c_{1, 2}
c_{2, 2}
\vdots
c_{n, 2} \end{bmatrix}\begin{bmatrix} l_{2, 1}, l_{2, 2}, \cdots, l_{2, m} \end{bmatrix} \end{align}
Que são dois produtos extermos somados. Que beleza, que maravilha. Agora, caso o primeiro produto externo seja independente linearmente do segundo, a matriz resultante tem posto dois. Observe que tem uma premissa um pouco forte aqui, porém garantias teóricas de SVD vão nos assegurar que os dois produtos externos são independentes.
No fim do dia SVD é apenas isto, uma forma de escrever matrizes como somas de produtos externos. Isto é interessante pois como cada produto externo captura fatores independentes dos outros, os mesmos codificam informações diferentes da nossa matriz. Do ponto de vista geral, temos:

A escolha de quantos produtos externos, ou posto final, será sua
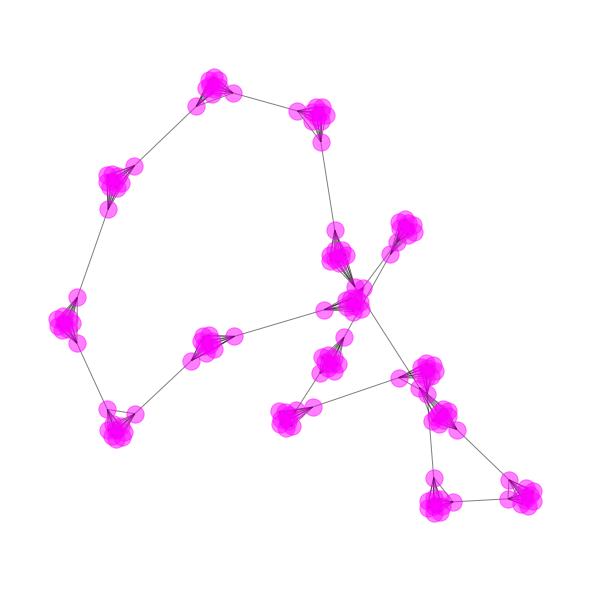
SVD em um Grafo
#In:
import networkx as nx
#In:
plt.figure(figsize=(8, 8))
G = nx.generators.community.ring_of_cliques(15, 10)
nx.draw_spring(G, node_color='magenta', alpha=0.5)
#In:
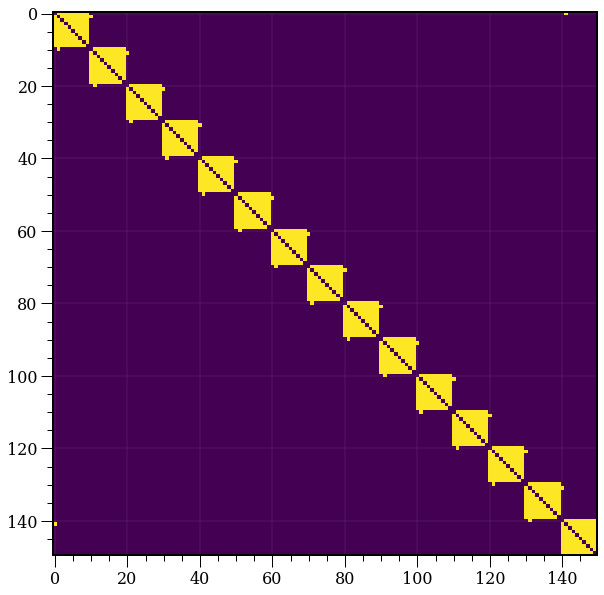
A = nx.adjacency_matrix(G).toarray()
plt.imshow(A)
<matplotlib.image.AxesImage at 0x7f1d8724db70>
#In:
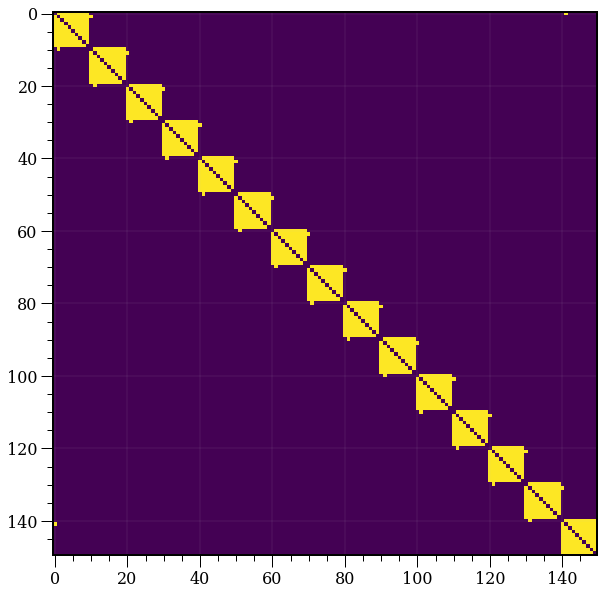
U, s, Vh = np.linalg.svd(A)
S = np.diag(s)
#In:
R = U.dot(S).dot(Vh)
plt.imshow(R)
<matplotlib.image.AxesImage at 0x7f1d854d30a0>
#In:
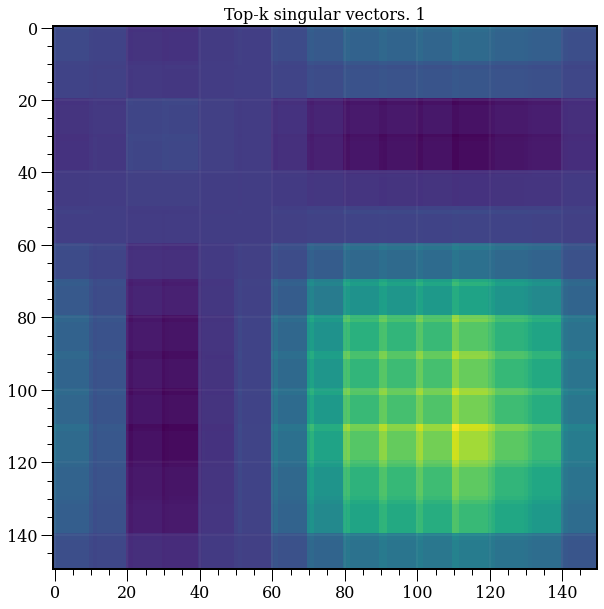
from sklearn.decomposition import TruncatedSVD
model = TruncatedSVD(n_components=1)
plt.title('Top-k singular vectors. {}'.format(1))
T = model.fit_transform(A)
R = model.inverse_transform(T)
plt.imshow(R);
#In:
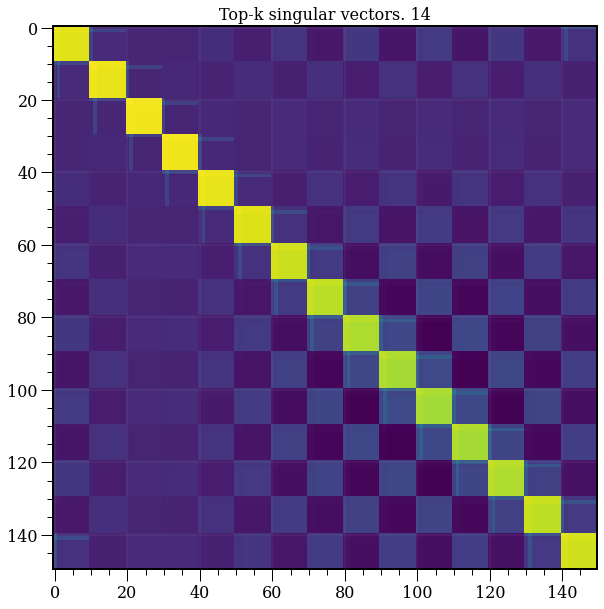
model = TruncatedSVD(n_components=14)
plt.title('Top-k singular vectors. {}'.format(14))
T = model.fit_transform(A)
R = model.inverse_transform(T)
plt.imshow(R);
#In:
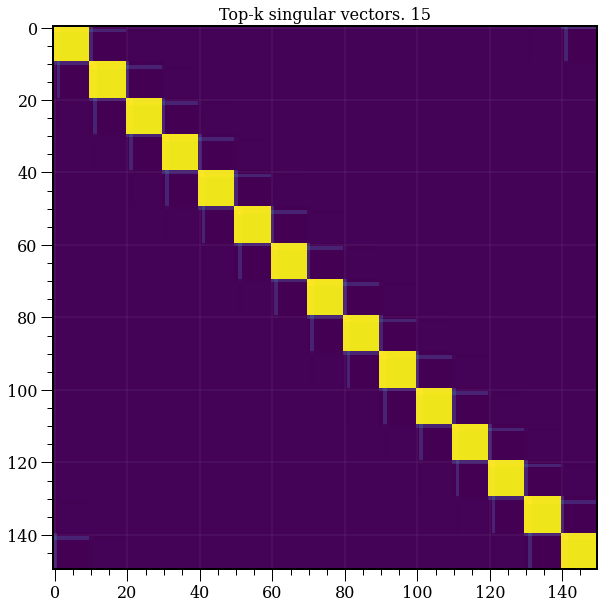
model = TruncatedSVD(n_components=15)
plt.title('Top-k singular vectors. {}'.format(15))
T = model.fit_transform(A)
R = model.inverse_transform(T)
plt.imshow(R);
#In:
from IPython.display import HTML
from matplotlib import animation
#In:
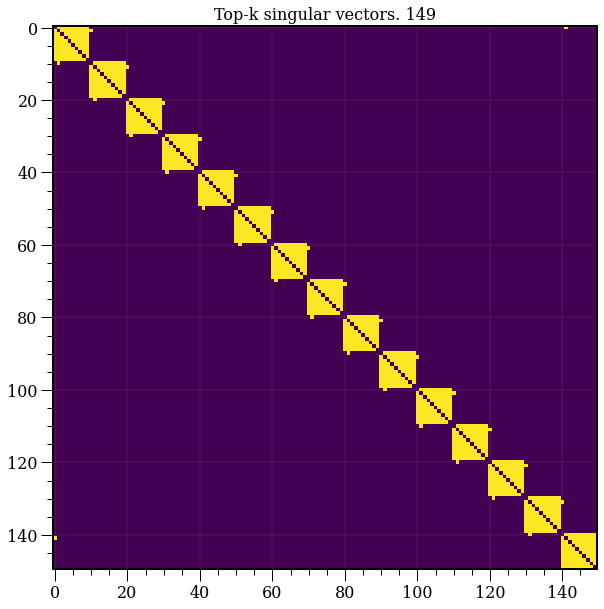
def plot(k):
plt.cla()
model = TruncatedSVD(n_components=k+1)
plt.title('Top-k singular vectors. {}'.format(k+1))
T = model.fit_transform(A)
R = model.inverse_transform(T)
plt.imshow(R)
fig = plt.figure()
ani = animation.FuncAnimation(fig, plot, len(A)-1)
HTML(ani.to_html5_video())
SVD em Texto
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/24-Decomposicao/fixed_comments.csv', sep='\t')
del df['Unnamed: 0']
df.head()
| id | created_time | media_code | owner_username | mentioned_usernames | tags | |
|---|---|---|---|---|---|---|
| 0 | 17842640887345362 | 1547342805 | Bsjbn9igpY1 | alitawiiiiil | [''] | [''] |
| 1 | 17842690399347336 | 1547406553 | Bsk53uml3PU | tommypazz | ['thegirlwiththeironfists'] | [''] |
| 2 | 17842728391347487 | 1547379803 | Bsknsm4HUzX | dudhyanth85 | [''] | [''] |
| 3 | 17842732198347154 | 1547387905 | Bskx3OuHrR_ | scilliaanna | [''] | [''] |
| 4 | 17842740721347584 | 1547392787 | Bsk8XtWAf4H | davipinna | [''] | [''] |
#In:
from collections import defaultdict
users = {}
tags = {}
mentions = defaultdict(int)
pop_tags = defaultdict(int)
pop_users = defaultdict(int)
for user, tags_str in df[['owner_username', 'tags']].values:
for tag in tags_str[1:-1].replace("'", "").strip().split(','):
if tag.strip():
for cleaned in tag.split('#'):
cleaned = cleaned.strip()
if user not in users:
users[user] = len(users)
if cleaned not in tags:
tags[cleaned] = len(tags)
mentions[user, cleaned] += 1
pop_tags[cleaned] += 1
pop_users[user] += 1
inverse_users = dict((v, k) for k, v in users.items())
inverse_tags = dict((v, k) for k, v in tags.items())
#In:
from scipy import sparse as sp
X = sp.lil_matrix((len(users), len(tags)))
for user, tag in mentions:
X[users[user], tags[tag]] = np.log10(mentions[user, tag] + 1)
X = X.tocsr()
#In:
def print_top_words(model, feature_names):
for topic_idx, topic in enumerate(model.components_):
message = "Topic #%d: " % topic_idx
message += " ".join([feature_names[i]
for i in topic.argsort()[:-10 - 1:-1]])
print(message)
print()
#In:
model = TruncatedSVD(n_components=20)
model.fit_transform(X)
print_top_words(model, inverse_tags)
Topic #0: fashion style photooftheday love instagood ootd picoftheday outfit beautiful outfitoftheday
Topic #1: ootd outfitoftheday fashionista lookoftheday lookbook fashion fashiongram outfit ootdshare whatiwore
Topic #2: foodporn napolifoodporn napoli italyfoodporn food puokemed pizza instafood foodblogger foodie
Topic #3: igersitalia ig_italia italia whatitalyis italy italian_places italiainunoscatto instaitalia ilikeitaly roma
Topic #4: valespo valespotour velespo catania valessi napoli valerio angel sespo valespi
Topic #5: likeforlike follow4follow follow igers f4f like4like likeforfollow whatiworetoday likeforlikes whatiwore
Topic #6: fitness love fit workout motivation gym whatiwore whatiworetoday bodybuilding ootdshare
Topic #7: instagood picoftheday instamood instafashion instadaily pretty fashionista bestoftheday igdaily instacool
Topic #8: love milano italy napoli amore milan roma naples inspiration frasi
Topic #9: frasi leggere libri aforismi citazioni amore parole poetry poesia reading
Topic #10: fashionblogger travel blogger travelgram style fashion tagsforlikes instatravel trip fashionaddict
Topic #11: italy milan milano seriea forzamilan football italia acmilan weareacmilan rossoneri
Topic #12: photooftheday lookbook instagood fashiondiaries followme fashiongram fashionpost travel love like4like
Topic #13: fashionblogger blogger fashionaddict fashionblog fashionlover fashionista instalike streetstyle fashiondaily like4like
Topic #14: love newsuominiedonne anticipazionitv tronoclassico anticipazioniuominiedonne tronoclassicoinformazioni francescochiofalo mariadefilippi saraaffifella anticipazioni
Topic #15: ootd newsuominiedonne anticipazionitv likeback tronoclassico anticipazioniuominiedonne instamood tronoclassicoinformazioni igdaily francescochiofalo
Topic #16: italianfood homedecor cucinaitaliana cucina interior design pasta pranzo piattiitaliani interiordesign
Topic #17: homedecor hm interior bershka tezenis oysho calzedonia stradivarius mango design
Topic #18: design homedecor style interior interiordesign instadesign instahome arredarecasa decorazioni amazing
Topic #19: leggere bookstagram reading instabook booklovers italianfood bookworm booklover bookaddict libro
SVD em Áudio
Escute o aúdio abaixo, quantos timbres diferentes você consegue identificar?*
Como você já deve ter percebido, o aúdio é um pequeno trecho de uma bateria. Você deve ouvir ao menos três timbres:
- Um bumbo, fazendo “tu”
- Uma caixa, fazendo “pa”
- Um chimbal, fazendo “ts”
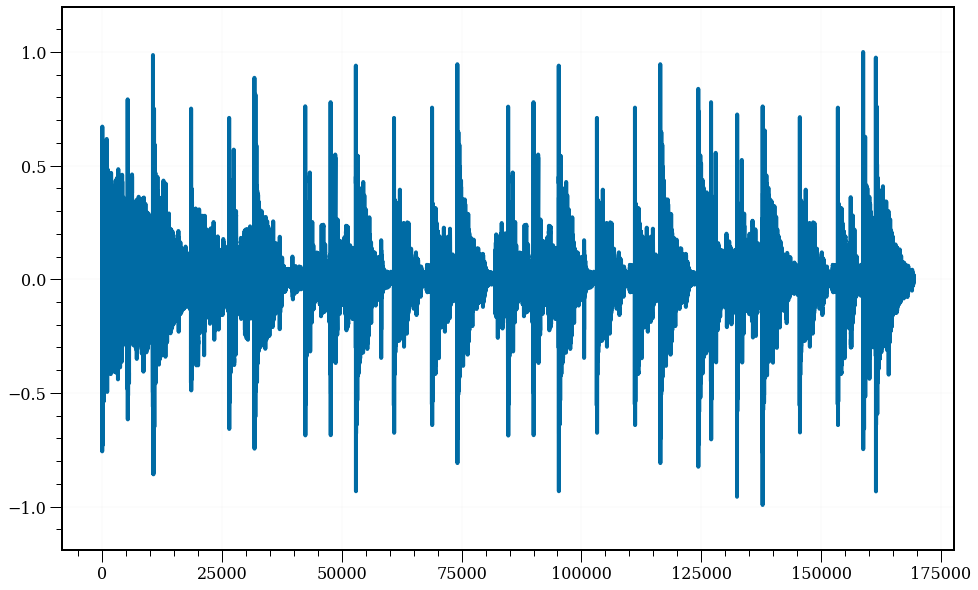
O interessante da bateria é que o momento qual cada tambor ou prato é tocado fica bem ressaltado, vide o plot abaixo.
#In:
! wget --no-check-certificate http://dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav
--2022-07-04 13:10:13-- http://dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav
Resolving dcc.ufmg.br (dcc.ufmg.br)... 150.164.0.135
Connecting to dcc.ufmg.br (dcc.ufmg.br)|150.164.0.135|:80... connected.
HTTP request sent, awaiting response... 302 Found
Location: https://dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav [following]
--2022-07-04 13:10:13-- https://dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav
Loaded CA certificate '/etc/ssl/certs/ca-certificates.crt'
Connecting to dcc.ufmg.br (dcc.ufmg.br)|150.164.0.135|:443... connected.
HTTP request sent, awaiting response... 302 Found
Location: https://homepages.dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav [following]
--2022-07-04 13:10:13-- https://homepages.dcc.ufmg.br/~flaviovdf/mir/examples/drum.wav
Resolving homepages.dcc.ufmg.br (homepages.dcc.ufmg.br)... 150.164.0.136
Connecting to homepages.dcc.ufmg.br (homepages.dcc.ufmg.br)|150.164.0.136|:443... connected.
WARNING: The certificate of ‘homepages.dcc.ufmg.br’ is not trusted.
WARNING: The certificate of ‘homepages.dcc.ufmg.br’ doesn't have a known issuer.
HTTP request sent, awaiting response... 200 OK
Length: 338732 (331K) [audio/x-wav]
Saving to: ‘drum.wav.3’
drum.wav.3 100%[===================>] 330.79K 1.42MB/s in 0.2s
2022-07-04 13:10:14 (1.42 MB/s) - ‘drum.wav.3’ saved [338732/338732]
#In:
import librosa
import librosa.display
import IPython.display as ipd
wav, sr = librosa.load('drum.wav')
ipd.Audio(wav, rate=sr)
#In:
plt.plot(wav);
SVD como um problema de otimização
Agora voltando para SVD. Observe como o espectrograma é uma matriz de valores complexas (vide slides).
#In:
S = librosa.stft(wav)
S[1, 0]
(10.508328+0.7458785j)
#In:
S.real
array([[-1.0217804e+01, -4.2669902e+00, 8.5735732e-01, ...,
2.8654882e-03, 2.0271653e-02, 7.3598772e-02],
[ 1.0508328e+01, -9.2004836e-01, -5.0310057e-01, ...,
-2.0415775e-02, 2.5208871e-04, -1.3964828e-02],
[-1.3302649e+01, 5.7067213e+00, 2.2181463e+00, ...,
1.9810859e-02, 1.6776076e-02, -8.2778484e-02],
...,
[-3.6144343e-03, 1.8340437e-03, 5.5644057e-05, ...,
2.5990506e-05, 2.5369343e-04, -1.1420063e-03],
[ 3.5729280e-03, -4.7158138e-04, -2.3402879e-04, ...,
-1.9609588e-04, -1.9089393e-04, -6.0880888e-04],
[-3.4242067e-03, -1.1065764e-03, 3.5329279e-04, ...,
3.1900464e-04, 4.6339084e-04, 1.6451691e-03]], dtype=float32)
#In:
S.imag
array([[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[ 7.45878518e-01, 5.37424612e+00, -2.40619093e-01, ...,
-5.81824174e-03, 1.17106745e-02, 4.83954363e-02],
[ 2.38943230e-02, 2.91091657e+00, -4.18579519e-01, ...,
3.12329270e-02, -3.98629867e-02, -3.16173304e-03],
...,
[ 4.81380150e-04, 1.28406327e-05, -2.96440732e-04, ...,
-1.33546608e-04, 2.36461110e-05, 1.00734876e-03],
[-4.07548767e-04, -1.86706556e-03, 3.75182688e-04, ...,
-8.70139629e-05, 1.47516732e-06, -1.18747598e-03],
[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00]], dtype=float32)
Como é comum, vamos trabalhar na norma do número complexo. Assim, fazemos uso de np.abs para pegar tal norma. Isto é, sendo $z$ o valor complexo, $z = a + i\cdot b$, então sua norma é $ | z | = \sqrt{a^2 + b^2}$. |
Vamos guardar também o ângulo. Teremos um uso para o mesmo no futuro.
#In:
X = np.abs(S)
A = np.angle(S)
#In:
def plot_spec(X, fig=None, ax=None, color=True):
'''Aqui X tem que ser o absoluto'''
if fig is None and ax is None:
fig, ax = plt.subplots()
X_db = librosa.amplitude_to_db(X, ref=np.max)
img = librosa.display.specshow(X_db, x_axis='time', y_axis='log', ax=ax)
if color:
fig.colorbar(img, ax=ax, format="%+2.f dB");
#In:
plot_spec(X);
/tmp/ipykernel_23759/2223863282.py:10: MatplotlibDeprecationWarning: Auto-removal of grids by pcolor() and pcolormesh() is deprecated since 3.5 and will be removed two minor releases later; please call grid(False) first.
fig.colorbar(img, ax=ax, format="%+2.f dB");
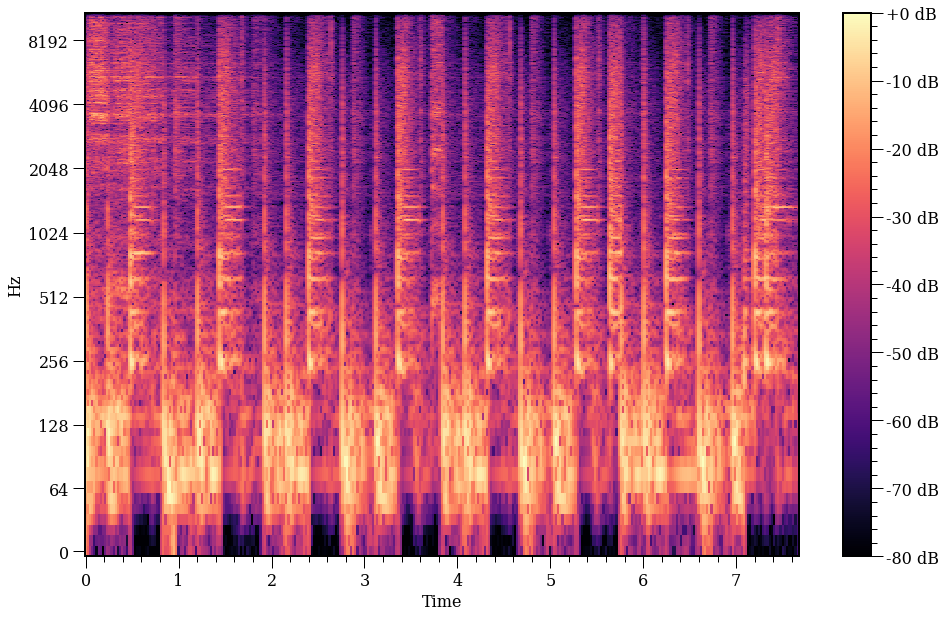
Agora vamos decompor o espectrograma. A bateria tem uma série de informação que se repete, abaixo tentei ressaltar algumas partes.

Parece que algums frequências aparecem mais em alguns tempos. Primeiro temos frequências baixa, depois alta, depois baixa. Tu, pa, tu, pa…. Além disso deve ter um ts, ts, ts constante por aí. O importante é. INFORMAÇÃO REDUNDANTE. Que ferramenta bacana aprendemos para achar tal informação?
Otimizando SVD
Observe que podemos re-escrever nossa definição de SVD da seguinte forma:
\[U_s V^{t} - X = \mathbf{0}\]Onde, $\mathbf{0}$ é uma matriz do mesmo tamanho de X, porém composta apenas de zeros. Ora, se a diferença acima é a matriz de zeros, isto quer dizer que a norma dos dois lados (isto vai valer para qualquer norma) tem que ser zero!
\[|| U_s V^{t} - X || = || \mathbf{0} ||\]Você já deve estar pensando, ok, vou otimizar alguma coisa. Portando, vamos trabalhar com normas ponto-a-ponto:
\[|| U_s V^{t} - X ||_{p} = 0\]Onde a norma é definida como:
\[|| M \|_{p} = \left( \sum_{i=1}^n \sum_{j=1}^m |a_{i,j}|^p \right)^{1/p}\]Vamos fazer uso da norma $p=2$ e elevar ao quadrado, tudo é mais fácil ao quadrado. E no fim do dia é um pouco por isso mesmo.
\[|| U_s V^{t} - X ||^2_{2} = \sum_{i=1}^n \sum_{j=1}^m ( (U_s V^{t})_{i,j} - X_{i,j})^2 = 0\]Uma soma de quadrados. Que lindo. Conhecemos os dados $X$, nosso espectrograma. Desconhecemos $U_s$ e $V$. Como achar? Deriva, otimiza, seja feliz.
Ao invés de derivar, vamos de sklearn.
#In:
from sklearn.decomposition import TruncatedSVD
k = 5
model = TruncatedSVD(n_components=k)
#In:
U = model.fit_transform(X)
sigma = np.diag(model.singular_values_)
V = model.components_
plot_spec(U @ sigma @ V);
/tmp/ipykernel_23759/2223863282.py:10: MatplotlibDeprecationWarning: Auto-removal of grids by pcolor() and pcolormesh() is deprecated since 3.5 and will be removed two minor releases later; please call grid(False) first.
fig.colorbar(img, ax=ax, format="%+2.f dB");
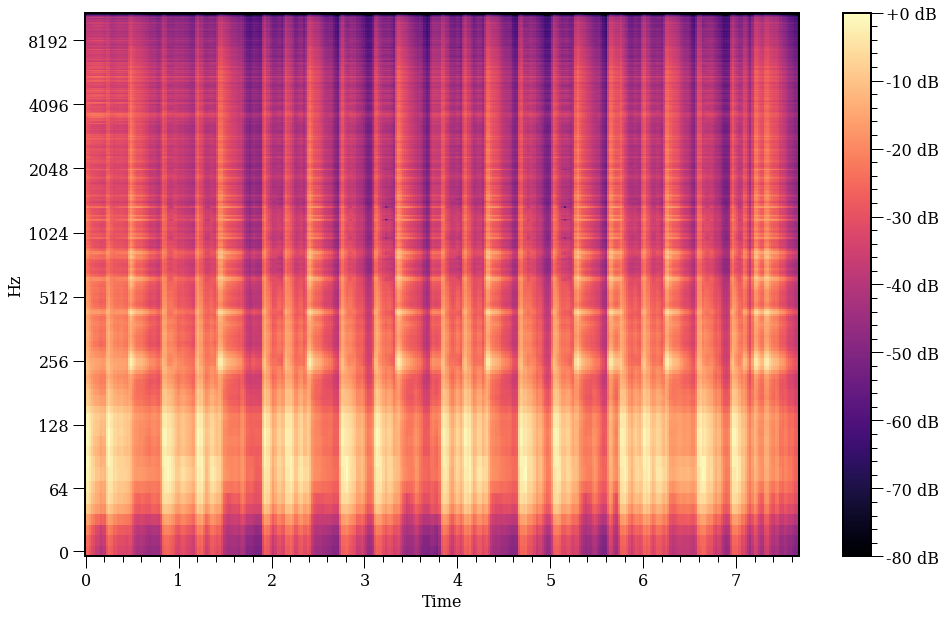
#In:
U = model.fit_transform(X)
sigma = np.diag(model.singular_values_)
V = model.components_
def recover_from_one(U, sigma, V, factor):
right = U[:, factor][:, np.newaxis]
s = sigma[factor, factor]
left = V[factor][np.newaxis]
return (right @ left) * s
#In:
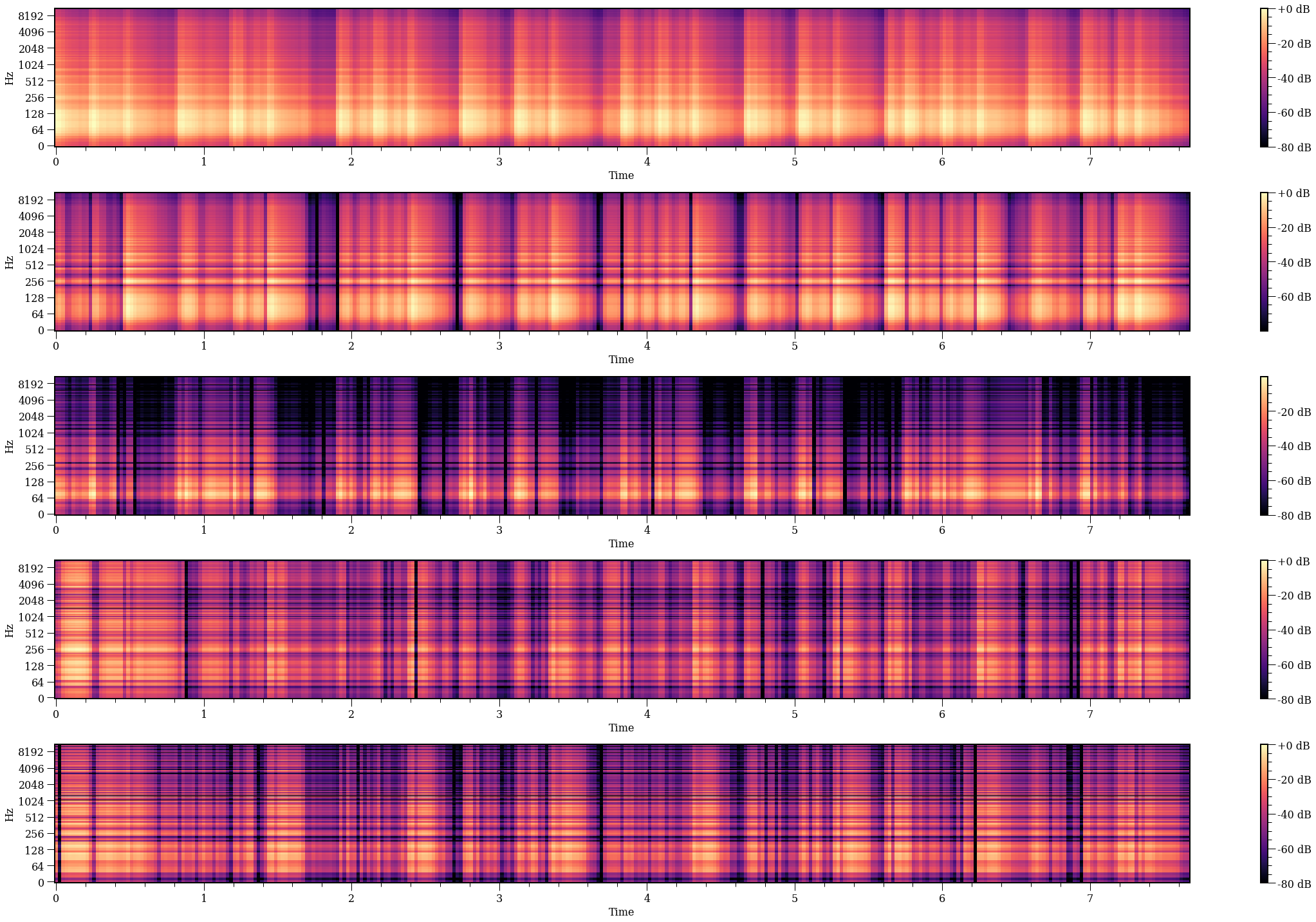
fig, axes = plt.subplots(k, 1, figsize=(32, 20))
for i in range(k):
X_model = recover_from_one(U, sigma, V, i)
plot_spec(X_model, fig, axes[i])
fig.tight_layout()
/tmp/ipykernel_23759/2223863282.py:10: MatplotlibDeprecationWarning: Auto-removal of grids by pcolor() and pcolormesh() is deprecated since 3.5 and will be removed two minor releases later; please call grid(False) first.
fig.colorbar(img, ax=ax, format="%+2.f dB");
#In:
X_model = recover_from_one(U, sigma, V, 0)
S_model = X_model * np.exp(1j * A)
wav_model = librosa.istft(np.asarray(S_model))
ipd.Audio(wav_model, rate=sr)
#In:
X_model = recover_from_one(U, sigma, V, 1)
S_model = X_model * np.exp(1j * A)
wav_model = librosa.istft(np.asarray(S_model))
ipd.Audio(wav_model, rate=sr)
#In:
X_model = recover_from_one(U, sigma, V, 2)
S_model = X_model * np.exp(1j * A)
wav_model = librosa.istft(np.asarray(S_model))
ipd.Audio(wav_model, rate=sr)
#In:
X_model = recover_from_one(U, sigma, V, 2)
S_model = X_model * np.exp(1j * A)
wav_model = librosa.istft(np.asarray(S_model))
ipd.Audio(wav_model, rate=sr)
#In:
X_model = recover_from_one(U, sigma, V, 4)
S_model = X_model * np.exp(1j * A)
wav_model = librosa.istft(np.asarray(S_model))
ipd.Audio(wav_model, rate=sr)
PCA
#In:
from sklearn.decomposition import PCA
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/24-Decomposicao/capes-cacc.csv', index_col=3).fillna(0)
del df['Programa']
del df['Instituição']
nivel = df['Nível']
del df['Nível']
df = pd.get_dummies(df, columns=['Tem doutorado'], drop_first=False)
df.head()
| Docentes colaboradores | Docentes permanentes | Docentes visitantes | Resumos em conf | Resumos expandidos em conf | Artigos em conf | Dissertacoes | Teses | periodicos_A1 | periodicos_A2 | ... | per_comaluno_A2 | per_comaluno_B1 | per_comaluno_B2 | per_comaluno_B3 | per_comaluno_B4 | per_comaluno_B5 | per_comaluno_C | per_comaluno_NA | Tem doutorado_Não | Tem doutorado_Sim | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sigla | |||||||||||||||||||||
| UFAM | 0.25 | 24.75 | 0.0 | 20 | 25 | 390 | 108.0 | 14.0 | 15 | 19 | ... | 5.0 | 4.0 | 0.0 | 2.0 | 0.0 | 5.0 | 6.0 | 6.0 | 0 | 1 |
| UFPA | 5.50 | 14.00 | 0.0 | 23 | 24 | 284 | 77.0 | 0.0 | 19 | 21 | ... | 5.0 | 2.0 | 1.0 | 2.0 | 0.0 | 0.0 | 5.0 | 14.0 | 0 | 1 |
| UFMA | 3.00 | 10.00 | 0.0 | 15 | 7 | 115 | 50.0 | 0.0 | 5 | 11 | ... | 5.0 | 5.0 | 1.0 | 0.0 | 0.0 | 4.0 | 3.0 | 2.0 | 1 | 0 |
| UEMA | 6.25 | 14.00 | 0.0 | 5 | 10 | 73 | 25.0 | 0.0 | 1 | 1 | ... | 0.0 | 2.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 2.0 | 1 | 0 |
| FUFPI | 1.75 | 9.50 | 0.0 | 4 | 1 | 150 | 31.0 | 0.0 | 7 | 4 | ... | 2.0 | 2.0 | 0.0 | 0.0 | 2.0 | 8.0 | 2.0 | 9.0 | 1 | 0 |
5 rows × 28 columns
#In:
Z = (df - df.mean()) / df.std(ddof=1)
Z
| Docentes colaboradores | Docentes permanentes | Docentes visitantes | Resumos em conf | Resumos expandidos em conf | Artigos em conf | Dissertacoes | Teses | periodicos_A1 | periodicos_A2 | ... | per_comaluno_A2 | per_comaluno_B1 | per_comaluno_B2 | per_comaluno_B3 | per_comaluno_B4 | per_comaluno_B5 | per_comaluno_C | per_comaluno_NA | Tem doutorado_Não | Tem doutorado_Sim | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sigla | |||||||||||||||||||||
| UFAM | -0.942673 | 0.366255 | -0.290455 | -0.171810 | -0.255158 | 0.818448 | 0.538385 | -0.018267 | -0.227736 | 0.066281 | ... | -0.117974 | -0.279284 | -0.564571 | -0.262590 | -0.584528 | 0.318601 | 0.215795 | -0.133150 | -1.090781 | 1.090781 |
| UFPA | 0.380598 | -0.503534 | -0.290455 | -0.060084 | -0.285247 | 0.241514 | 0.050755 | -0.474934 | -0.088021 | 0.158338 | ... | -0.117974 | -0.478772 | 0.015468 | -0.262590 | -0.584528 | -0.830200 | 0.015985 | 1.115132 | -1.090781 | 1.090781 |
| UFMA | -0.249531 | -0.827176 | -0.290455 | -0.358020 | -0.796766 | -0.678314 | -0.373954 | -0.474934 | -0.577024 | -0.301946 | ... | -0.117974 | -0.179540 | 0.015468 | -0.630706 | -0.584528 | 0.088841 | -0.383635 | -0.757291 | 0.904550 | -0.904550 |
| UEMA | 0.569636 | -0.503534 | -0.290455 | -0.730440 | -0.706498 | -0.906911 | -0.767204 | -0.474934 | -0.716739 | -0.762231 | ... | -0.569406 | -0.478772 | -0.564571 | -0.446648 | -0.584528 | -0.830200 | -0.783255 | -0.757291 | 0.904550 | -0.904550 |
| FUFPI | -0.564595 | -0.867632 | -0.290455 | -0.767682 | -0.977302 | -0.487817 | -0.672824 | -0.474934 | -0.507166 | -0.624145 | ... | -0.388833 | -0.478772 | -0.564571 | -0.630706 | 0.668032 | 1.007882 | -0.583445 | 0.334956 | 0.904550 | -0.904550 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| UFMS/UFG | -1.005685 | -0.726038 | 3.340236 | -0.618714 | -0.525962 | -0.422504 | -1.160454 | -0.018267 | -0.262665 | 0.066281 | ... | -0.569406 | -0.578517 | -0.564571 | -0.630706 | -0.584528 | -0.140920 | -0.983065 | -0.757291 | -1.090781 | 1.090781 |
| UFMS/CA/Prof | 0.758675 | -0.503534 | -0.290455 | -0.395262 | -0.525962 | -0.912353 | -0.955964 | -0.474934 | -0.716739 | -0.762231 | ... | -0.569406 | -0.678261 | -0.564571 | -0.630706 | -0.584528 | -0.830200 | -0.983065 | -1.069362 | 0.904550 | -0.904550 |
| UFG | -0.060492 | 0.871947 | 1.524890 | -0.209052 | -0.315336 | -0.008854 | 0.444005 | -0.474934 | -0.437308 | -0.071804 | ... | -0.027688 | -0.179540 | 0.595507 | 0.105527 | 1.294311 | -0.140920 | 0.815225 | -0.133150 | 0.904550 | -0.904550 |
| UNB | -0.942673 | 0.265117 | -0.290455 | -0.246294 | -0.646319 | -0.014296 | -0.216654 | -0.050886 | 0.086623 | -0.301946 | ... | -0.479120 | 0.718158 | 0.595507 | -0.446648 | 1.294311 | 0.318601 | 1.214845 | 0.022885 | -1.090781 | 1.090781 |
| UNB/CA/Prof | 1.262778 | -0.442851 | -0.290455 | -0.879408 | -0.887034 | -0.890582 | -0.373954 | -0.474934 | -0.751668 | -0.808259 | ... | -0.569406 | -0.678261 | -0.564571 | -0.446648 | 0.041752 | -0.830200 | -0.983065 | -1.069362 | 0.904550 | -0.904550 |
75 rows × 28 columns
#In:
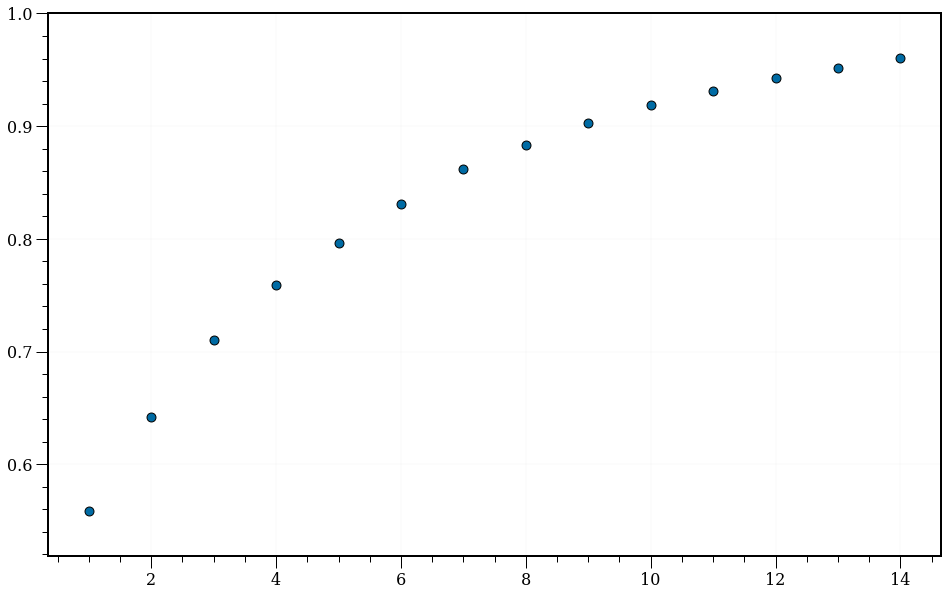
components = list(range(1, 15))
y = []
for k in components:
pca = PCA(n_components=k)
pca = pca.fit(Z)
y.append(pca.explained_variance_ratio_.sum())
plt.scatter(components, y, s=80, edgecolors='k')
<matplotlib.collections.PathCollection at 0x7f1d7d15b280>
#In:
plt.figure(figsize=(20, 20))
pca = PCA(n_components=2)
pca = pca.fit(Z)
N = pca.transform(Z)
plt.scatter(N[:, 0], N[:, 1], s=0, edgecolors='k')
ax = plt.gca()
for i, txt in enumerate(df.index):
ax.annotate('{}.{}'.format(txt, nivel[i]), (N[:, 0][i], N[:, 1][i]))

#In: