Verossimilhança
Entendimento de relação entre dados.
Resultados Esperados
- Revisitar os mínimos quadrados (ALC)
- Entender a regressão linear do ponto de vista probabilístico
- Entender o conceito de verossimilhança
Sumário
#In:
# -*- coding: utf8
from scipy import stats as ss
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
#In:
plt.ion()
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Continuando da aula passada. Vamos ver mais uma forma de entender um modelo de regressão linear. Lembre-se até agora falamos de correlação e covariância cobrindo os seguintes tópicos:
- Covariância
- Coeficiente de Pearson (Covariância Normalizada)
- Coeficiente de Pearson como sendo a fração do desvio de y capturado por x
- Mínimos Quadrados
Todos os passos acima chegam no mesmo local de traçar a “melhor” reta no gráfico de dispersão. Melhor aqui significa a reta que que minimiza o erro abaixo:
\(\Theta = [\alpha, \beta]\) \(L(\Theta) = \sum_i (y_i - \hat{y}_i)^2\) \(L(\Theta) = \sum_i (y_i - \beta x_i + \alpha)^2\)
Chegamos em:
\begin{align} \alpha & = \bar{y} - \beta\,\bar{x}, \[5pt] \beta &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 } \[6pt] &= \frac{ \operatorname{Cov}(x, y) }{ \operatorname{Var}(x) } \[5pt] &= r_{xy} \frac{s_y}{s_x}. \[6pt] \end{align}
Visão probabílistica
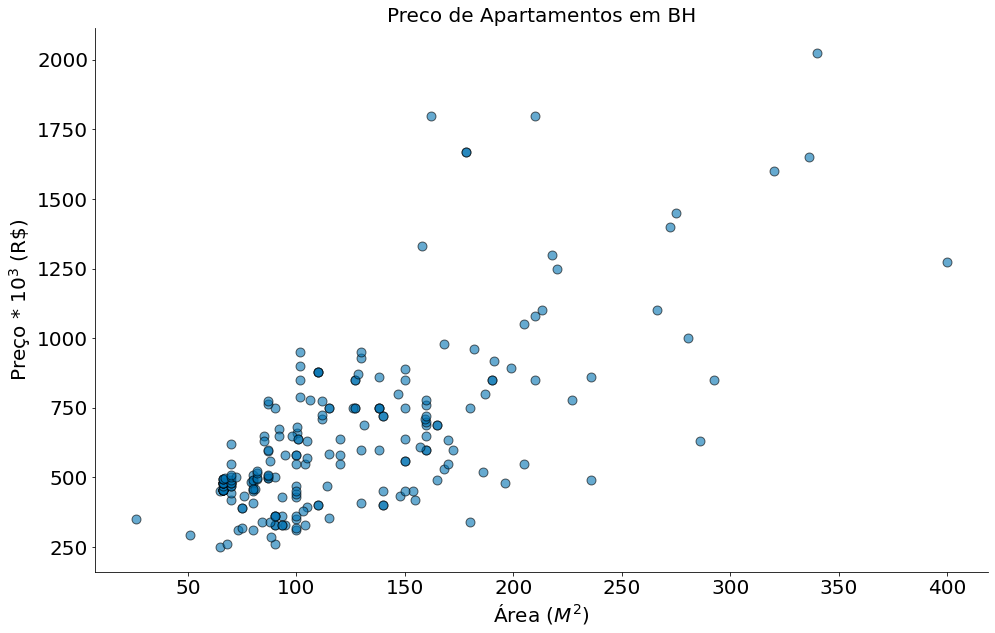
Vamos aprender uma última forma de pensar na regressão. Em particular, vamos fazer uso de uma visão probabílistica. Para tal, exploraremos o caso dos apartamentos de BH abaixo.
Inicialmente, vamos observar os dados além do resultado da melhor regressão.
#In:
df = pd.read_csv('https://raw.githubusercontent.com/icd-ufmg/material/master/aulas/17-Verossimilhanca/aptosBH.txt', index_col=0)
df['preco'] = df['preco'] / 1000
plt.scatter(df['area'], df['preco'], edgecolors='k', s=80, alpha=0.6)
plt.title('Preco de Apartamentos em BH')
plt.ylabel(r'Preço * $10^3$ (R\$)')
plt.xlabel(r'Área ($M^2$)')
despine()
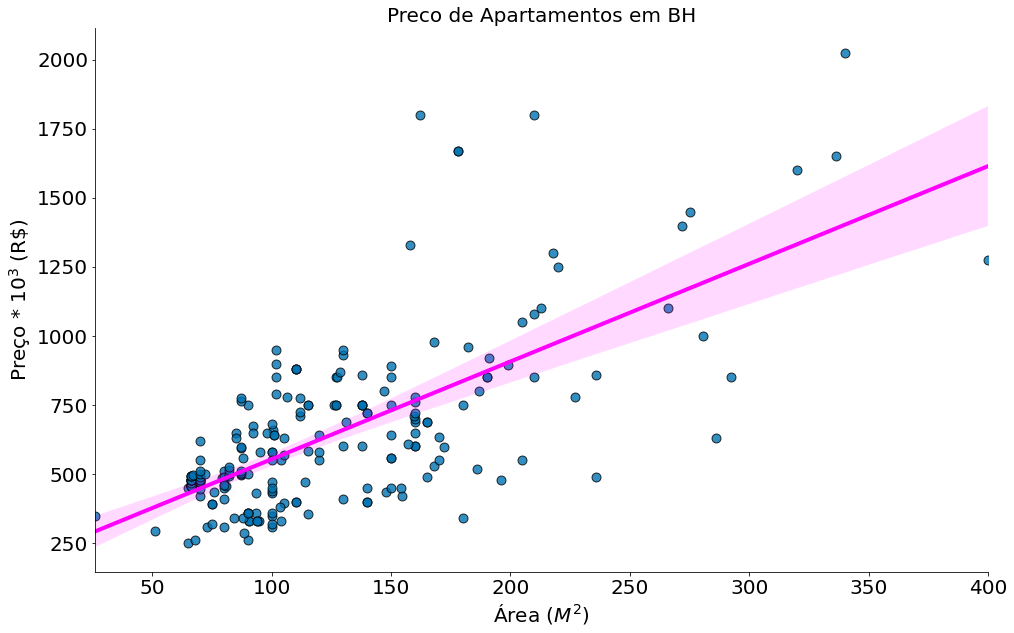
O seaborn tem uma função regplot que plota a melhor reta além de um IC (estmado via bootstrap – aula passada).
#In:
sns.regplot(x='area', y='preco', data=df, n_boot=10000,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.title('Preco de Apartamentos em BH')
plt.ylabel(r'Preço * $10^3$ (R\$)')
plt.xlabel(r'Área ($M^2$)')
despine()
A reta pode ser recuperada usando scipy.
#In:
model = ss.linregress(df['area'], df['preco'])
# beta = slope
# alpha = intercept
model
LinregressResult(slope=3.5357191563336516, intercept=200.5236136898945, rvalue=0.694605637960645, pvalue=1.917920339304322e-32, stderr=0.2503210673009473)
Usando esta reta podemos prever o preço de um apartamento usando apenas a área do mesmo.
#In:
beta = model.slope
alpha = model.intercept
novo_apt_area = 225
preco = beta * novo_apt_area + alpha
preco
996.0604238649662
Ou seja, quando um apartamento de 225m2 entra no mercado o mesmo custa em torno de 1M de reais.
Erros Normais
Agora, será que conseguimos chegar no mesmo pensando na regressão como um modelo probabilístico?
#In:
x = np.linspace(-5, 5, 100)
plt.plot(x, ss.distributions.norm.pdf(x, scale=1))
plt.xlabel(r'$\epsilon_i$')
plt.ylabel(r'$p(\epsilon_i \mid \mu=0, \sigma=1)$')
despine()
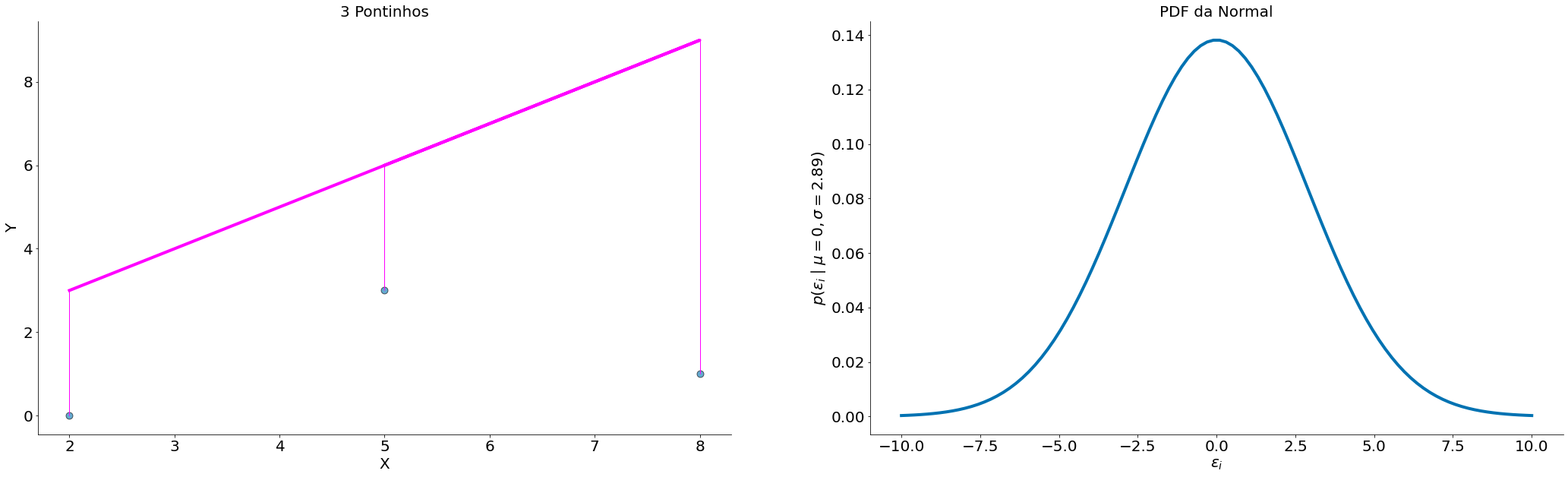
#In:
beta = 1
alpha = 1
fig = plt.figure(figsize=(36, 10))
x = np.array([2, 8, 5])
y = np.array([0, 1, 3])
plt.subplot(121)
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('3 Pontinhos')
plt.ylabel(r'Y')
plt.xlabel(r'X')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
plt.subplot(122)
plt.title('PDF da Normal')
ei_x = np.linspace(-10, 10, 100)
sigma = (y - y_bar).std(ddof=1)
plt.plot(ei_x, ss.distributions.norm.pdf(ei_x, scale=sigma))
plt.xlabel(r'$\epsilon_i$')
plt.ylabel(r'$p(\epsilon_i \mid \mu=0, \sigma={})$'.format(np.round(sigma, 2)))
despine()
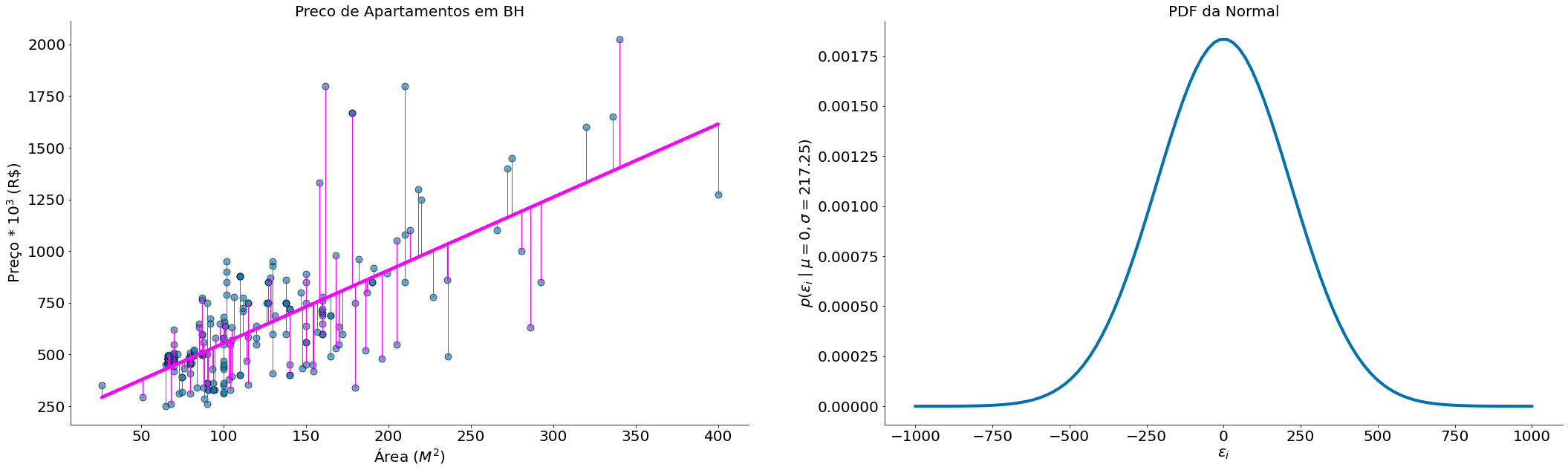
#In:
beta = 3.535719156333653
alpha = 200.52361368989432
fig = plt.figure(figsize=(36, 10))
x = df['area']
y = df['preco']
plt.subplot(121)
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('Preco de Apartamentos em BH')
plt.ylabel(r'Preço * $10^3$ (R\$)')
plt.xlabel(r'Área ($M^2$)')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
plt.subplot(122)
plt.title('PDF da Normal')
ei_x = np.linspace(-1000, 1000, 100)
sigma = (y - y_bar).std(ddof=1)
plt.plot(ei_x, ss.distributions.norm.pdf(ei_x, scale=sigma))
plt.xlabel(r'$\epsilon_i$')
plt.ylabel(r'$p(\epsilon_i \mid \mu=0, \sigma={})$'.format(np.round(sigma, 2)))
despine()
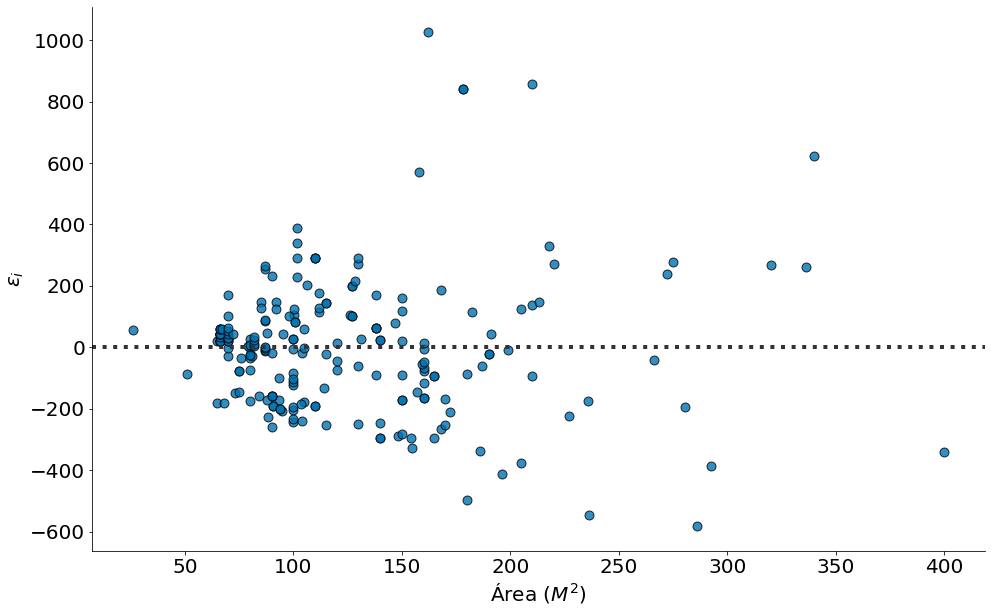
#In:
sns.residplot(x='area', y='preco', data=df,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.ylabel(r'$\epsilon_i$')
plt.xlabel(r'Área ($M^2$)')
despine()
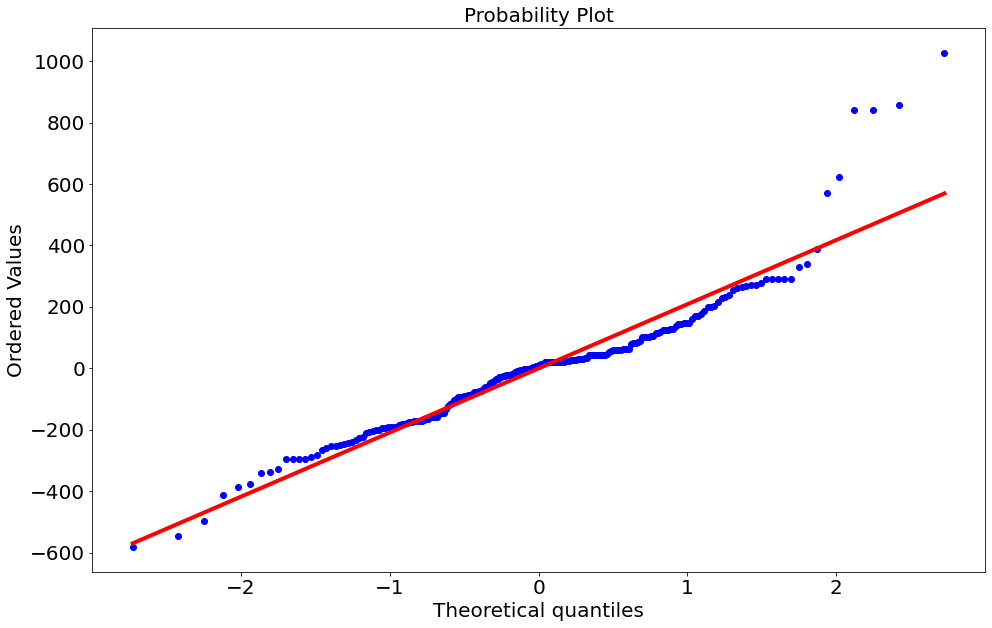
#In:
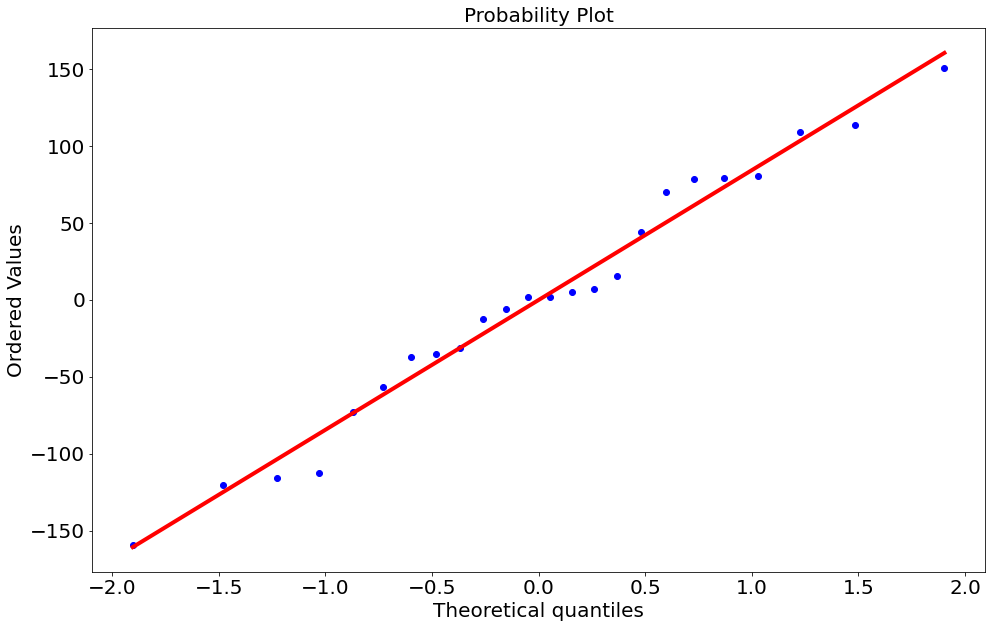
ss.probplot(y - y_bar, plot=plt.gca());
((array([-2.72615229, -2.41925291, -2.24456515, -2.11960108, -2.02096546,
-1.93878946, -1.86793868, -1.80538627, -1.74919165, -1.69803298,
-1.65096767, -1.6072989 , -1.56649638, -1.5281468 , -1.49192147,
-1.45755452, -1.42482771, -1.39355955, -1.36359747, -1.33481187,
-1.3070917 , -1.28034108, -1.25447654, -1.22942504, -1.20512221,
-1.18151106, -1.15854082, -1.13616613, -1.11434623, -1.09304437,
-1.07222728, -1.05186477, -1.0319293 , -1.01239573, -0.99324101,
-0.97444395, -0.95598503, -0.93784624, -0.92001088, -0.90246348,
-0.88518965, -0.868176 , -0.85141001, -0.83488001, -0.81857505,
-0.80248485, -0.78659978, -0.77091076, -0.75540925, -0.74008717,
-0.7249369 , -0.70995122, -0.69512332, -0.6804467 , -0.6659152 ,
-0.65152299, -0.63726449, -0.62313438, -0.60912761, -0.59523934,
-0.58146495, -0.56780001, -0.55424028, -0.5407817 , -0.52742038,
-0.51415256, -0.50097464, -0.48788315, -0.47487475, -0.46194622,
-0.44909444, -0.43631642, -0.42360925, -0.41097012, -0.3983963 ,
-0.38588516, -0.37343413, -0.36104072, -0.34870253, -0.3364172 ,
-0.32418243, -0.311996 , -0.29985573, -0.2877595 , -0.27570523,
-0.26369089, -0.25171449, -0.23977409, -0.22786778, -0.21599368,
-0.20414996, -0.19233481, -0.18054645, -0.16878313, -0.15704311,
-0.14532471, -0.13362622, -0.121946 , -0.11028238, -0.09863376,
-0.0869985 , -0.07537501, -0.06376169, -0.05215696, -0.04055926,
-0.02896701, -0.01737865, -0.00579262, 0.00579262, 0.01737865,
0.02896701, 0.04055926, 0.05215696, 0.06376169, 0.07537501,
0.0869985 , 0.09863376, 0.11028238, 0.121946 , 0.13362622,
0.14532471, 0.15704311, 0.16878313, 0.18054645, 0.19233481,
0.20414996, 0.21599368, 0.22786778, 0.23977409, 0.25171449,
0.26369089, 0.27570523, 0.2877595 , 0.29985573, 0.311996 ,
0.32418243, 0.3364172 , 0.34870253, 0.36104072, 0.37343413,
0.38588516, 0.3983963 , 0.41097012, 0.42360925, 0.43631642,
0.44909444, 0.46194622, 0.47487475, 0.48788315, 0.50097464,
0.51415256, 0.52742038, 0.5407817 , 0.55424028, 0.56780001,
0.58146495, 0.59523934, 0.60912761, 0.62313438, 0.63726449,
0.65152299, 0.6659152 , 0.6804467 , 0.69512332, 0.70995122,
0.7249369 , 0.74008717, 0.75540925, 0.77091076, 0.78659978,
0.80248485, 0.81857505, 0.83488001, 0.85141001, 0.868176 ,
0.88518965, 0.90246348, 0.92001088, 0.93784624, 0.95598503,
0.97444395, 0.99324101, 1.01239573, 1.0319293 , 1.05186477,
1.07222728, 1.09304437, 1.11434623, 1.13616613, 1.15854082,
1.18151106, 1.20512221, 1.22942504, 1.25447654, 1.28034108,
1.3070917 , 1.33481187, 1.36359747, 1.39355955, 1.42482771,
1.45755452, 1.49192147, 1.5281468 , 1.56649638, 1.6072989 ,
1.65096767, 1.69803298, 1.74919165, 1.80538627, 1.86793868,
1.93878946, 2.02096546, 2.11960108, 2.24456515, 2.41925291,
2.72615229]),
array([-581.7392924 , -544.95333458, -496.95306183, -413.52456833,
-384.93361007, -375.34604074, -339.81127622, -338.16737677,
-327.3932956 , -295.52429558, -295.52429558, -295.02436377,
-293.91727448, -288.81004883, -280.88148714, -264.52443195,
-258.73833776, -252.13131667, -251.59587027, -250.16710401,
-245.52429558, -244.09552932, -238.23840595, -234.09552932,
-228.01047273, -223.69757724, -210.66730858, -205.56836094,
-204.09552932, -201.60835549, -201.60835549, -194.09552932,
-192.68176615, -190.15262542, -190.15262542, -189.45272089,
-189.45272089, -185.76340254, -180.95251632, -180.34535885,
-176.7741251 , -174.42297671, -173.3811462 , -171.63154226,
-171.36085515, -170.88148714, -170.88148714, -166.59587027,
-166.2386787 , -166.2386787 , -158.73833776, -158.73833776,
-158.73833776, -157.52402282, -148.6311121 , -145.70255041,
-145.63152123, -133.59559751, -124.09552932, -116.2386787 ,
-114.09552932, -104.09552932, -100.68906851, -93.91727448,
-93.91727448, -93.02463652, -90.88148714, -88.45285726,
-86.95306183, -86.37564854, -84.09552932, -76.2386787 ,
-75.70255041, -75.70255041, -74.80991245, -73.3811462 ,
-66.2386787 , -61.70309592, -60.16710401, -54.08189002,
-46.2386787 , -44.80991245, -41.02490927, -34.23826957,
-33.3811462 , -28.17436433, -28.02395463, -23.3811462 ,
-23.3811462 , -22.31025339, -22.31025339, -22.13131667,
-18.73833776, -18.23840595, -11.59082378, -9.59082378,
-9.1317258 , -6.2386787 , -4.09552932, -3.59082378,
-3.3811462 , -3.02395463, -1.7741251 , 1.40917622,
4.46777268, 5.15457296, 6.6188538 , 6.6188538 ,
9.36577268, 13.7613213 , 15.19008755, 19.11851286,
19.65464115, 21.41177816, 21.41177816, 21.41177816,
21.41177816, 21.41177816, 21.41177816, 21.41177816,
21.41177816, 21.97604537, 21.97604537, 24.14777268,
24.47570442, 24.47570442, 25.90447068, 25.90447068,
26.29717683, 26.6188538 , 31.97604537, 31.97604537,
31.97604537, 31.97604537, 33.41177816, 34.47477268,
41.97604537, 43.58306646, 44.05603446, 44.15402745,
44.41177816, 44.41177816, 44.41177816, 44.41177816,
44.41177816, 44.41177816, 48.33310055, 51.97604537,
57.54768825, 58.2258749 , 58.41177816, 58.41177816,
58.41177816, 59.40657284, 61.54714274, 61.54714274,
61.54714274, 61.97604537, 80.11459944, 82.51018029,
82.51018029, 86.40917622, 90.40917622, 100.44005346,
100.44005346, 101.97604537, 102.97590899, 103.97577261,
104.63161178, 113.4758408 , 115.62192794, 119.11851286,
124.19022393, 124.65395926, 125.02054089, 128.4758408 ,
128.94025802, 136.97536348, 142.86868333, 142.86868333,
146.36820601, 148.94025802, 149.19022393, 159.11851286,
171.54714274, 171.97604537, 178.4758408 , 185.47556805,
199.66219524, 200.44005346, 203.41729684, 215.03040315,
229.22196147, 231.26166224, 237.76077579, 256.40917622,
260.62617718, 266.40917622, 268.04625628, 269.83289599,
271.61817192, 277.15361832, 289.22196147, 289.83289599,
290.54727911, 290.54727911, 290.54727911, 328.68961023,
339.22196147, 389.22196147, 570.83275961, 622.33187316,
840.11837648, 840.11837648, 856.97536348, 1026.68988298])),
(208.8589454277071, 8.64308059430921e-14, 0.9535520964832741))
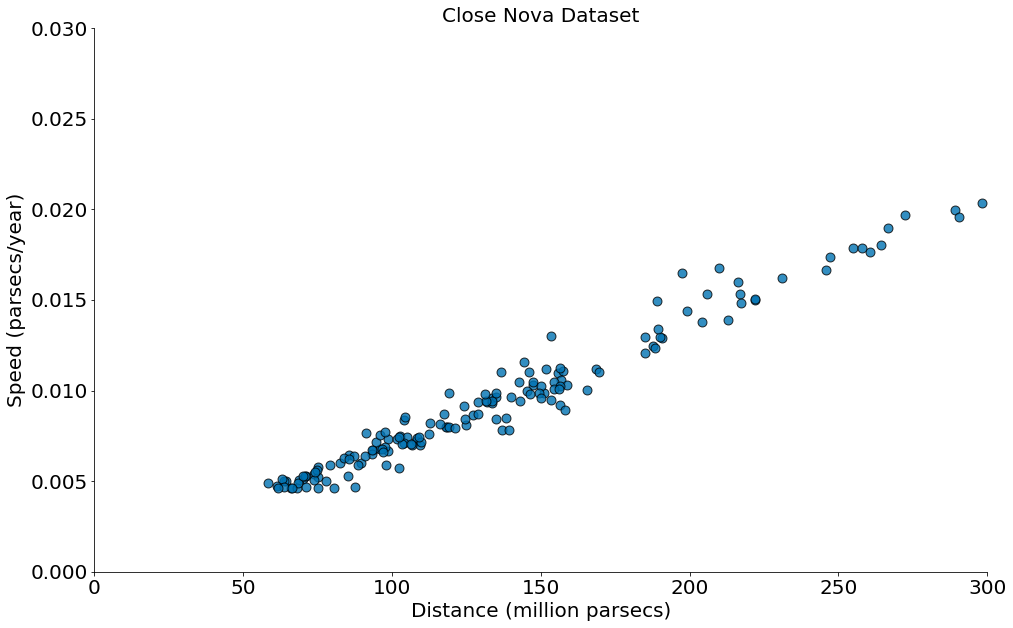
Close Nova Dataset
Abaixo temos a dispersão dos dados
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/17-Verossimilhanca/close_novas.csv')
x = df.values[:, 0]
y = df.values[:, 1]
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.xlabel(df.columns[0])
plt.ylabel(df.columns[1])
plt.xlim((0, 300))
plt.ylim((0, 0.03))
plt.title('Close Nova Dataset')
despine()
#In:
1e6 / (ss.pearsonr(x, y)[0] * y.std(ddof=1) / x.std(ddof=1))
14612822334.220728
#In:
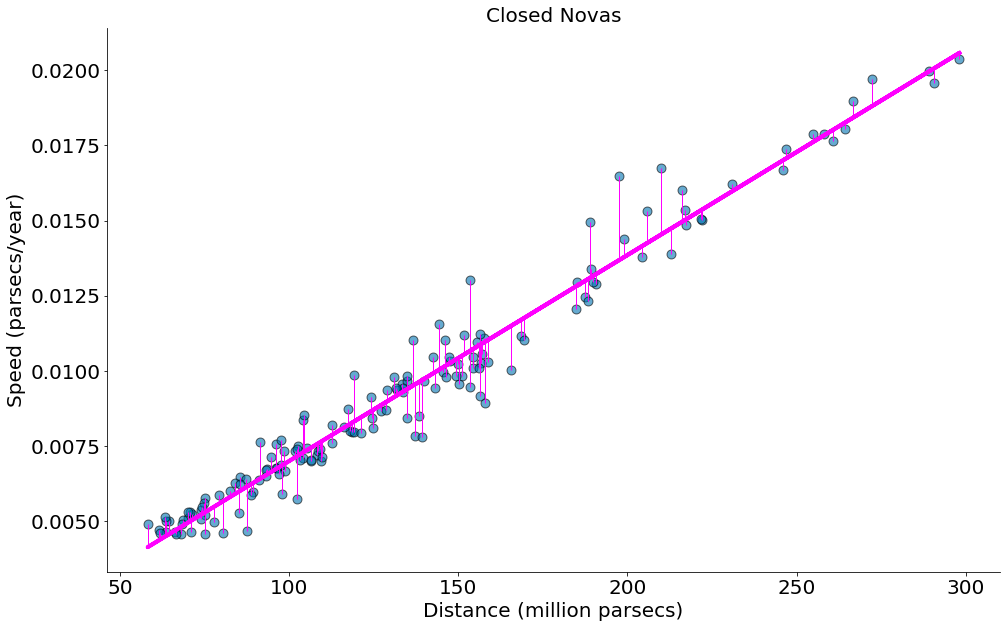
x = df['Distance (million parsecs)']
y = df['Speed (parsecs/year)']
model = ss.linregress(x, y)
beta = model.slope
alpha = model.intercept
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('Closed Novas')
plt.ylabel(r'Speed (parsecs/year)')
plt.xlabel(r'Distance (million parsecs)')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
#In:
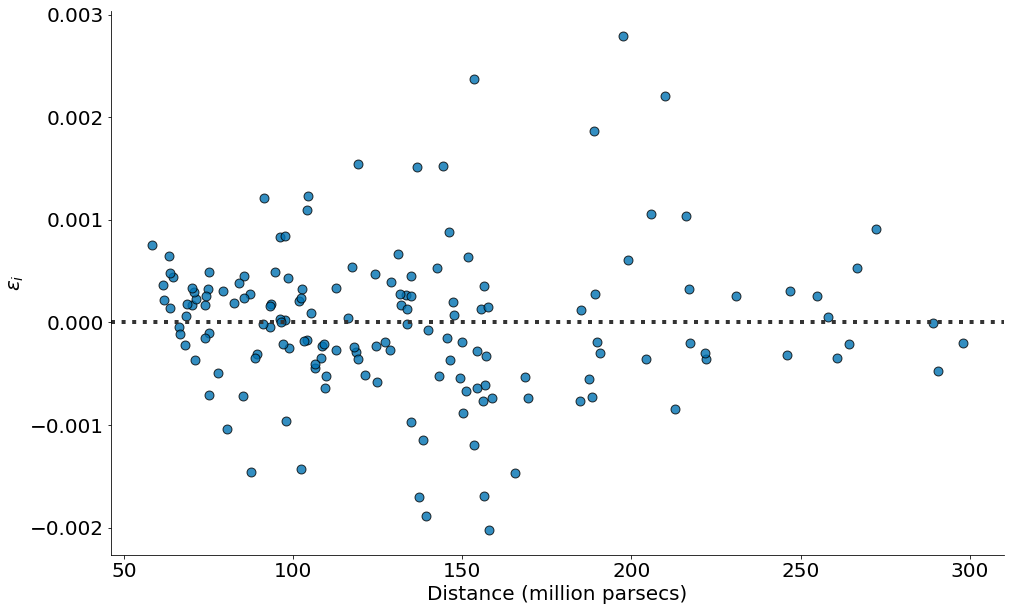
sns.residplot(x='Distance (million parsecs)', y='Speed (parsecs/year)', data=df,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.ylabel(r'$\epsilon_i$')
despine()
#In:
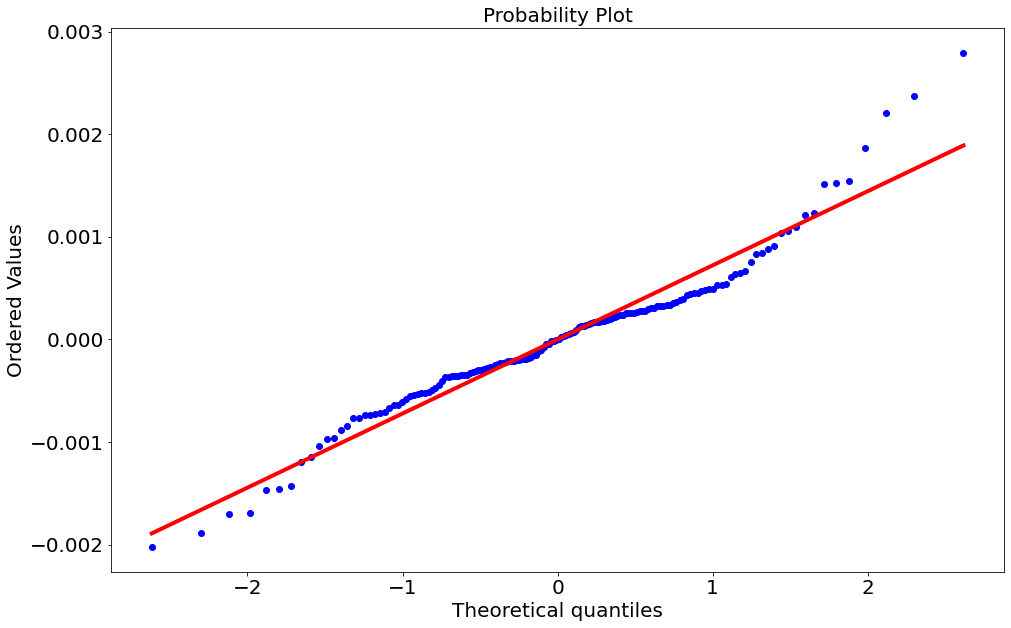
ss.probplot(y - y_bar, plot=plt);
((array([-2.61714799, -2.29873202, -2.11640064, -1.98538788, -1.88158842,
-1.79481923, -1.71977641, -1.65333021, -1.59347236, -1.53883391,
-1.48843794, -1.44156183, -1.39765528, -1.35628912, -1.31712186,
-1.27987709, -1.24432777, -1.21028503, -1.17758993, -1.14610741,
-1.11572166, -1.08633257, -1.05785299, -1.03020655, -1.0033259 ,
-0.97715135, -0.9516297 , -0.92671332, -0.90235939, -0.87852925,
-0.85518785, -0.83230334, -0.80984663, -0.78779108, -0.76611227,
-0.74478767, -0.7237965 , -0.70311953, -0.68273889, -0.66263799,
-0.64280133, -0.62321445, -0.60386381, -0.58473669, -0.56582115,
-0.54710594, -0.52858043, -0.51023459, -0.4920589 , -0.47404433,
-0.45618232, -0.43846468, -0.42088364, -0.40343174, -0.38610187,
-0.36888719, -0.35178115, -0.33477743, -0.31786997, -0.3010529 ,
-0.28432055, -0.26766742, -0.2510882 , -0.23457772, -0.21813094,
-0.20174296, -0.18540899, -0.16912433, -0.15288441, -0.13668471,
-0.1205208 , -0.10438832, -0.08828297, -0.07220048, -0.05613665,
-0.04008729, -0.02404825, -0.0080154 , 0.0080154 , 0.02404825,
0.04008729, 0.05613665, 0.07220048, 0.08828297, 0.10438832,
0.1205208 , 0.13668471, 0.15288441, 0.16912433, 0.18540899,
0.20174296, 0.21813094, 0.23457772, 0.2510882 , 0.26766742,
0.28432055, 0.3010529 , 0.31786997, 0.33477743, 0.35178115,
0.36888719, 0.38610187, 0.40343174, 0.42088364, 0.43846468,
0.45618232, 0.47404433, 0.4920589 , 0.51023459, 0.52858043,
0.54710594, 0.56582115, 0.58473669, 0.60386381, 0.62321445,
0.64280133, 0.66263799, 0.68273889, 0.70311953, 0.7237965 ,
0.74478767, 0.76611227, 0.78779108, 0.80984663, 0.83230334,
0.85518785, 0.87852925, 0.90235939, 0.92671332, 0.9516297 ,
0.97715135, 1.0033259 , 1.03020655, 1.05785299, 1.08633257,
1.11572166, 1.14610741, 1.17758993, 1.21028503, 1.24432777,
1.27987709, 1.31712186, 1.35628912, 1.39765528, 1.44156183,
1.48843794, 1.53883391, 1.59347236, 1.65333021, 1.71977641,
1.79481923, 1.88158842, 1.98538788, 2.11640064, 2.29873202,
2.61714799]),
array([-2.02379790e-03, -1.88382586e-03, -1.69877179e-03, -1.69171658e-03,
-1.46854729e-03, -1.45632481e-03, -1.43118117e-03, -1.19308513e-03,
-1.14299438e-03, -1.03860480e-03, -9.66239814e-04, -9.56636124e-04,
-8.78130311e-04, -8.46013759e-04, -7.70164376e-04, -7.63366122e-04,
-7.38923989e-04, -7.32074673e-04, -7.30279805e-04, -7.21866353e-04,
-7.11317289e-04, -6.64569386e-04, -6.39561386e-04, -6.39071968e-04,
-6.12688434e-04, -5.84989272e-04, -5.54950166e-04, -5.43245939e-04,
-5.27685042e-04, -5.21587236e-04, -5.21440051e-04, -5.14828899e-04,
-4.89786984e-04, -4.69661863e-04, -4.40780754e-04, -4.03047063e-04,
-3.70474363e-04, -3.70354876e-04, -3.53053803e-04, -3.52871761e-04,
-3.51743014e-04, -3.50591562e-04, -3.45131664e-04, -3.42469701e-04,
-3.27911447e-04, -3.22017926e-04, -3.07244491e-04, -3.02621606e-04,
-2.94923240e-04, -2.88685505e-04, -2.75431468e-04, -2.69799987e-04,
-2.64058127e-04, -2.46921766e-04, -2.44174108e-04, -2.33499856e-04,
-2.30820325e-04, -2.23774386e-04, -2.14740712e-04, -2.10131049e-04,
-2.06310685e-04, -2.05342571e-04, -2.00796535e-04, -1.95505237e-04,
-1.89871601e-04, -1.86875378e-04, -1.85290563e-04, -1.70200624e-04,
-1.54667380e-04, -1.48952569e-04, -1.13419340e-04, -9.85629293e-05,
-7.36289260e-05, -4.56484205e-05, -4.21780718e-05, -1.82781888e-05,
-1.71351293e-05, -6.24585746e-06, 6.14152384e-06, 2.17914673e-05,
3.82292260e-05, 4.53248426e-05, 4.90114626e-05, 6.02065660e-05,
7.19836485e-05, 8.99151259e-05, 1.16975919e-04, 1.33122068e-04,
1.33294352e-04, 1.41465772e-04, 1.50519890e-04, 1.63498022e-04,
1.69915884e-04, 1.71810122e-04, 1.74380020e-04, 1.76306177e-04,
1.82451934e-04, 1.88256460e-04, 2.02922063e-04, 2.05799701e-04,
2.20100033e-04, 2.29353201e-04, 2.37475716e-04, 2.37559899e-04,
2.53413236e-04, 2.53964396e-04, 2.56420865e-04, 2.57785972e-04,
2.64886779e-04, 2.72271192e-04, 2.76905267e-04, 2.81273800e-04,
2.92746719e-04, 3.04580650e-04, 3.06626484e-04, 3.22718933e-04,
3.23993822e-04, 3.24472954e-04, 3.36425448e-04, 3.37803251e-04,
3.50220173e-04, 3.63491050e-04, 3.80383577e-04, 3.98622833e-04,
4.31060852e-04, 4.37991110e-04, 4.48398048e-04, 4.50911597e-04,
4.69031413e-04, 4.84096743e-04, 4.94533310e-04, 4.96308797e-04,
5.29246319e-04, 5.31758017e-04, 5.39225429e-04, 6.12901108e-04,
6.33709790e-04, 6.42822591e-04, 6.69874529e-04, 7.55508460e-04,
8.28828000e-04, 8.45879913e-04, 8.81945180e-04, 9.09124622e-04,
1.04072154e-03, 1.05594477e-03, 1.09643546e-03, 1.21495608e-03,
1.23177119e-03, 1.51313815e-03, 1.52109514e-03, 1.53952527e-03,
1.86729798e-03, 2.21119941e-03, 2.36977275e-03, 2.79228144e-03])),
(0.0007222757798776553, -1.3575669791851328e-18, 0.9752858477835388))
#In:
import statsmodels.api as sm
stocks = {'Year': [2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016],
'Month': [12, 11,10,9,8,7,6,5,4,3,2,1,12,11,10,9,8,7,6,5,4,3,2,1],
'Interest_Rate': [2.75,2.5,2.5,2.5,2.5,2.5,2.5,2.25,2.25,2.25,2,2,2,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75],
'Unemployment_Rate': [5.3,5.3,5.3,5.3,5.4,5.6,5.5,5.5,5.5,5.6,5.7,5.9,6,5.9,5.8,6.1,6.2,6.1,6.1,6.1,5.9,6.2,6.2,6.1],
'Stock_Index_Price': [1464,1394,1357,1293,1256,1254,1234,1195,1159,1167,1130,1075,1047,965,943,958,971,949,884,866,876,822,704,719]
}
df = pd.DataFrame(stocks, columns=['Year','Month', 'Interest_Rate', 'Unemployment_Rate', 'Stock_Index_Price'])
#In:
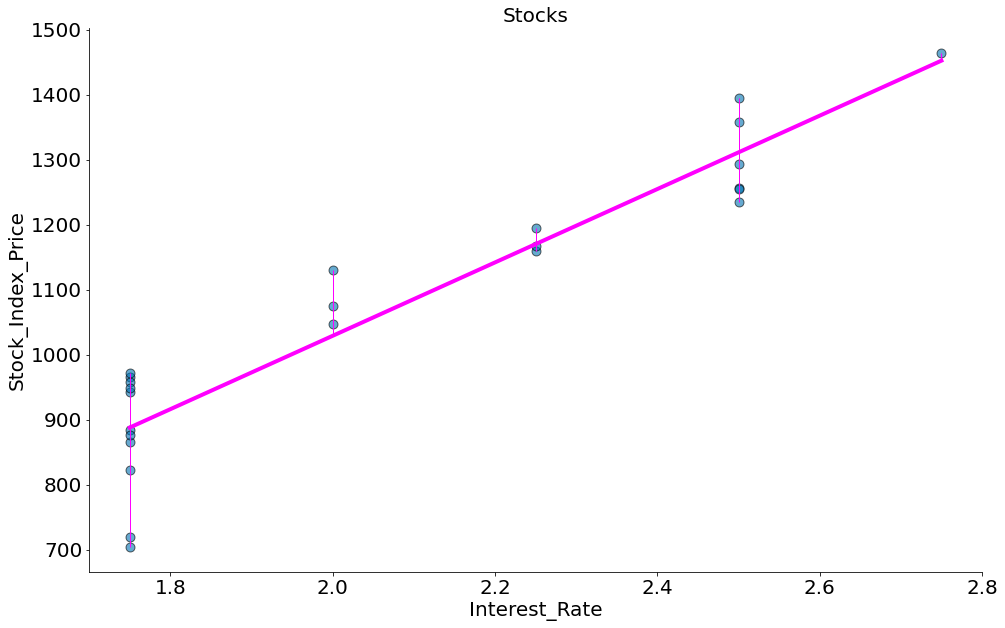
x = df['Interest_Rate']
y = df['Stock_Index_Price']
model = ss.linregress(x, y)
beta = model.slope
alpha = model.intercept
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('Stocks')
plt.ylabel(r'Stock_Index_Price')
plt.xlabel(r'Interest_Rate')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
#In:
sns.residplot(x='Interest_Rate', y='Stock_Index_Price', data=df,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.ylabel(r'$\epsilon_i$')
despine()
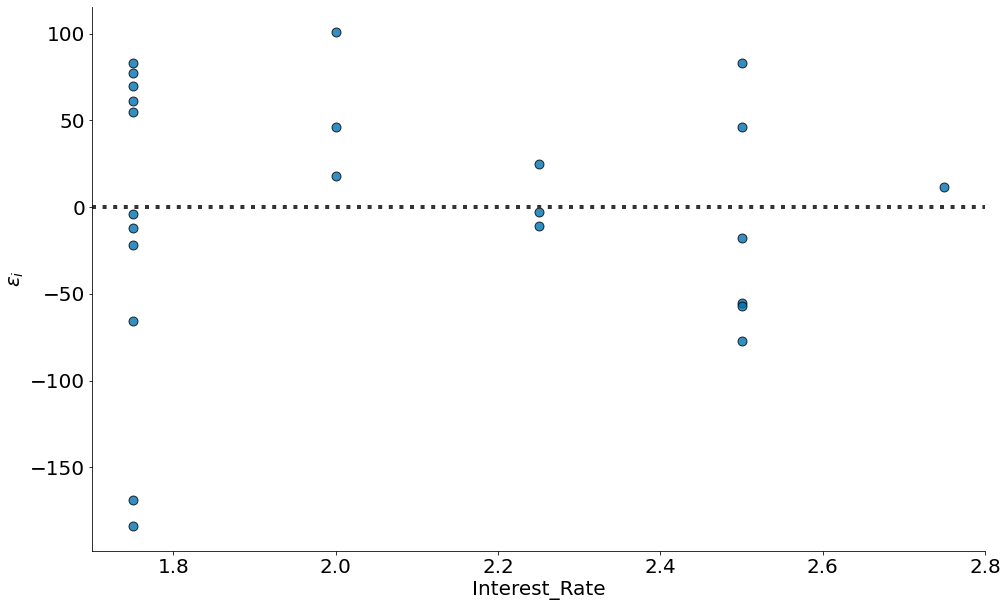
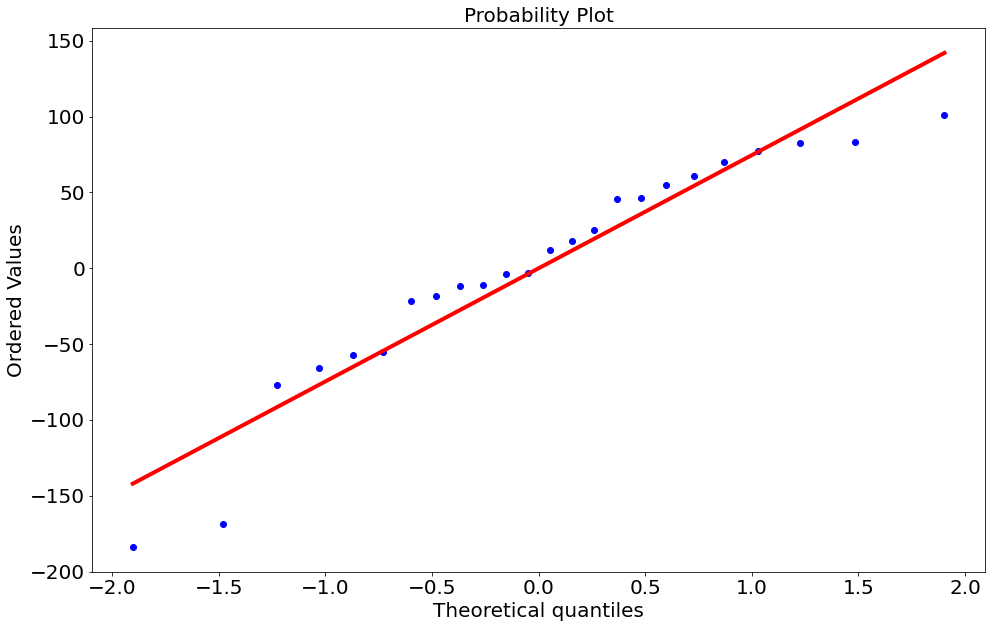
#In:
ss.probplot(y - y_bar, plot=plt);
((array([-1.90380091, -1.48287381, -1.22601535, -1.03156092, -0.8698858 ,
-0.7282709 , -0.59996024, -0.48085763, -0.36822879, -0.26009875,
-0.154935 , -0.05146182, 0.05146182, 0.154935 , 0.26009875,
0.36822879, 0.48085763, 0.59996024, 0.7282709 , 0.8698858 ,
1.03156092, 1.22601535, 1.48287381, 1.90380091]),
array([-183.89249305, -168.89249305, -77.04541242, -65.89249305,
-57.04541242, -55.04541242, -21.89249305, -18.04541242,
-11.89249305, -10.9944393 , -3.89249305, -2.9944393 ,
11.90361446, 18.05653383, 25.0055607 , 45.95458758,
46.05653383, 55.10750695, 61.10750695, 70.10750695,
77.10750695, 82.95458758, 83.10750695, 101.05653383])),
(74.6230273581124, -1.1664016504917942e-13, 0.9597002266879965))
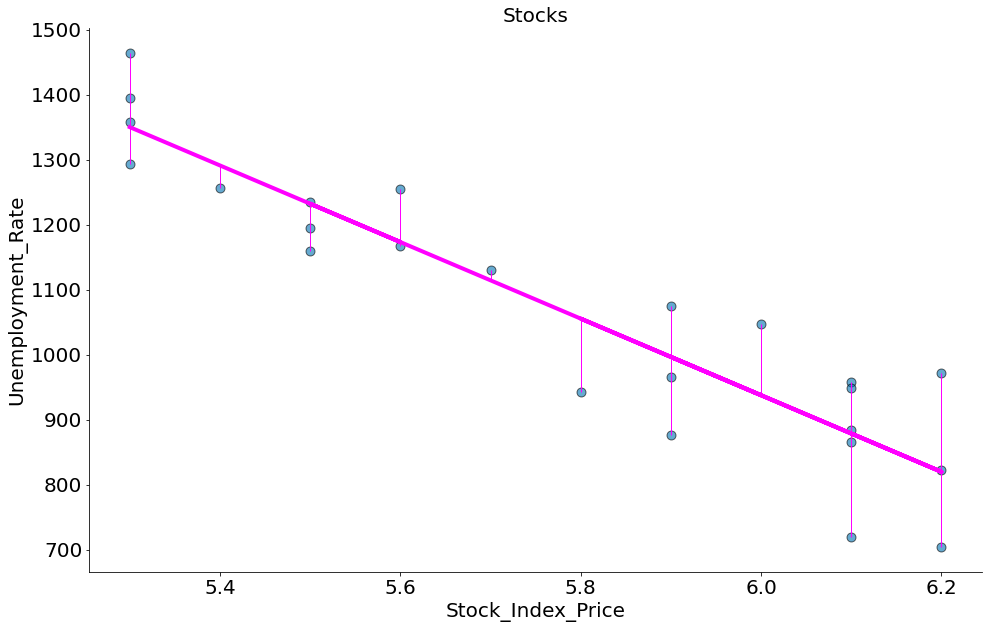
#In:
x = df['Unemployment_Rate']
y = df['Stock_Index_Price']
model = ss.linregress(x, y)
beta = model.slope
alpha = model.intercept
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('Stocks')
plt.ylabel(r'Unemployment_Rate')
plt.xlabel(r'Stock_Index_Price')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
#In:
sns.residplot(x='Unemployment_Rate', y='Stock_Index_Price', data=df,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.ylabel(r'$\epsilon_i$')
despine()
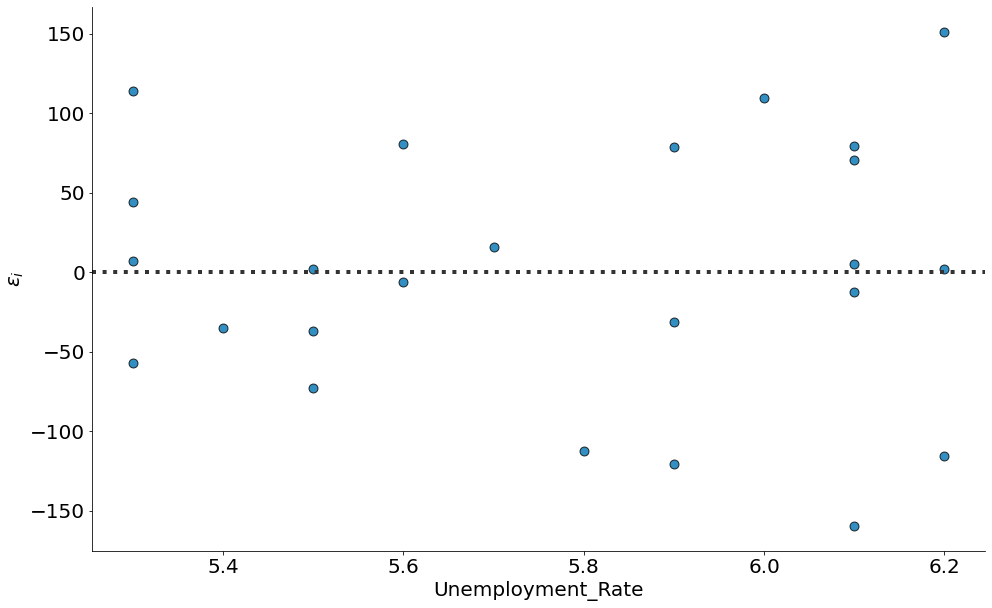
#In:
ss.probplot(y - y_bar, plot=plt);
((array([-1.90380091, -1.48287381, -1.22601535, -1.03156092, -0.8698858 ,
-0.7282709 , -0.59996024, -0.48085763, -0.36822879, -0.26009875,
-0.154935 , -0.05146182, 0.05146182, 0.154935 , 0.26009875,
0.36822879, 0.48085763, 0.59996024, 0.7282709 , 0.8698858 ,
1.03156092, 1.22601535, 1.48287381, 1.90380091]),
array([-159.67065868, -120.46307385, -115.7744511 , -112.35928144,
-73.04790419, -56.84031936, -37.04790419, -34.94411178,
-31.46307385, -12.67065868, -6.15169661, 1.95209581,
2.2255489 , 5.32934132, 7.15968064, 15.74451098,
44.15968064, 70.32934132, 78.53692615, 79.32934132,
80.84830339, 109.43313373, 114.15968064, 151.2255489 ])),
(84.44568675783013, -8.667143147774442e-13, 0.9909228257133791))
#In:
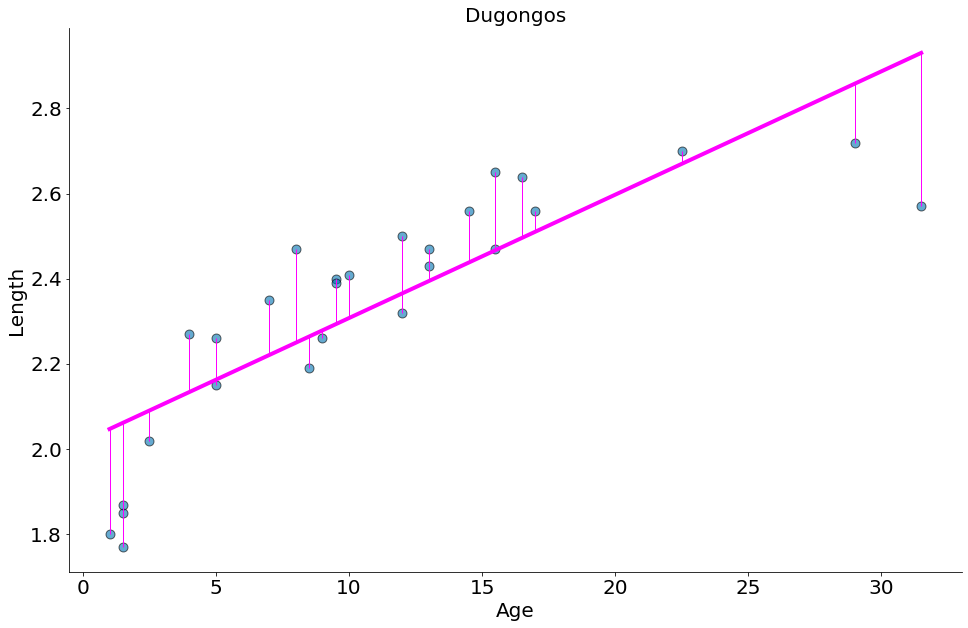
df = pd.read_csv('http://www.statsci.org/data/oz/dugongs.txt', sep='\t')
df
| Age | Length | |
|---|---|---|
| 0 | 1.0 | 1.80 |
| 1 | 1.5 | 1.85 |
| 2 | 1.5 | 1.87 |
| 3 | 1.5 | 1.77 |
| 4 | 2.5 | 2.02 |
| 5 | 4.0 | 2.27 |
| 6 | 5.0 | 2.15 |
| 7 | 5.0 | 2.26 |
| 8 | 7.0 | 2.35 |
| 9 | 8.0 | 2.47 |
| 10 | 8.5 | 2.19 |
| 11 | 9.0 | 2.26 |
| 12 | 9.5 | 2.40 |
| 13 | 9.5 | 2.39 |
| 14 | 10.0 | 2.41 |
| 15 | 12.0 | 2.50 |
| 16 | 12.0 | 2.32 |
| 17 | 13.0 | 2.43 |
| 18 | 13.0 | 2.47 |
| 19 | 14.5 | 2.56 |
| 20 | 15.5 | 2.65 |
| 21 | 15.5 | 2.47 |
| 22 | 16.5 | 2.64 |
| 23 | 17.0 | 2.56 |
| 24 | 22.5 | 2.70 |
| 25 | 29.0 | 2.72 |
| 26 | 31.5 | 2.57 |
#In:
x = df['Age']
y = df['Length']
model = ss.linregress(x, y)
beta = model.slope
alpha = model.intercept
plt.scatter(x, y, edgecolors='k', s=80, alpha=0.6)
plt.title('Dugongos')
plt.ylabel(r'Length')
plt.xlabel(r'Age')
y_bar = x * beta + alpha
plt.plot(x, y_bar, color='magenta')
y_min = [min(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
y_max = [max(y_i, y_bar_i) for y_i, y_bar_i in zip(y, y_bar)]
plt.vlines(x, ymin=y_min, ymax=y_max, color='magenta', lw=1)
despine()
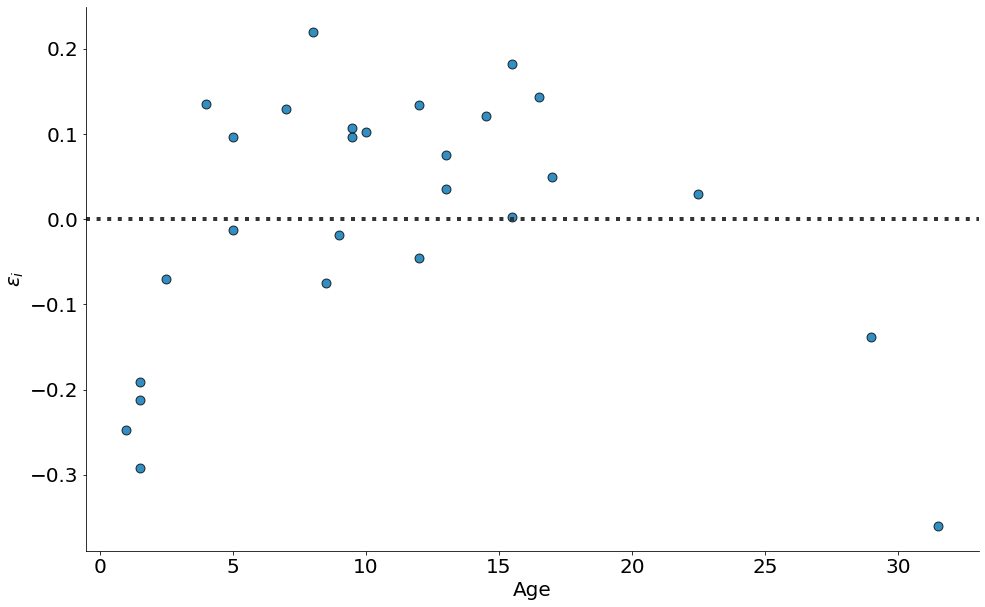
#In:
sns.residplot(x='Age', y='Length', data=df,
line_kws={'color':'magenta', 'lw':4},
scatter_kws={'edgecolor':'k', 's':80, 'alpha':0.8})
plt.ylabel(r'$\epsilon_i$')
despine()
#In:
df = pd.read_csv('http://www.statsci.org/data/oz/dugongs.txt', sep='\t')
y, x = df.values.T