Regressão Linear Simples
Entendimento de relação entre dados.
Resultados Esperados
- Revisitar os mínimos quadrados (ALC)
- Entender a regressão linear do ponto de vista estatístico (diferente de ALC)
- Entender o coeficiente de pearson e o R2.
- Executar regressões em python
Sumário
#In:
# -*- coding: utf8
from scipy import stats as ss
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
#In:
plt.ion()
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Antes de iniciar o nosso estudo da regressão, vamos pensar em um modelo que tenta capturar o valor médio no eixo y. Para uma base de dados unidimensional (apenas Y), a média ($\bar{y}$) é um bom estimador. Isto é, imagine que você está em uma sala de aula e entra um novo aluno na sala. Posso prever alguma característica deste aluno (por exemplo, o seu rendimento escolar) usando a média dos outros alunos em sala de aula.
Agora, como podemos proceder quando temos duas variáveis X e Y? Em uma aula anterior, usamos a função de correlação para medir a força da relação linear entre duas variáveis. Para a maioria das aplicações, saber que esse relacionamento linear existe não é suficiente. Queremos ser capazes de entender a natureza do relacionamento. É aqui que vamos usar a regressão linear simples.
Vamos olhar para uma bas bases dados que ajudaram a criar a regressão linear.
Poor Person’s KNN (Vizinhos Próximos Implementado de Forma Simples)
Vamos iniciar com a base de dados original analisada por Galton. Tal base captura altura de um filho, após alguns anos, com base na altura média dos pais. O problema sendo estudado era prever qual vai ser a altura futura de uma criança usando apenas a idade dos pais como entrada. Como temos um pai e uma mãe, usamos a média das alturas entre os dois. Então temos que:
- X é a altura média dos pais
- Y é a altura da criança após alguns anos (o mesmo número de anos para toda criança)
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/16-RegressaoLinear/galton.csv')
df.head()
| family | father | mother | midparentHeight | children | childNum | gender | childHeight | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 78.5 | 67.0 | 75.43 | 4 | 1 | male | 73.2 |
| 1 | 1 | 78.5 | 67.0 | 75.43 | 4 | 2 | female | 69.2 |
| 2 | 1 | 78.5 | 67.0 | 75.43 | 4 | 3 | female | 69.0 |
| 3 | 1 | 78.5 | 67.0 | 75.43 | 4 | 4 | female | 69.0 |
| 4 | 2 | 75.5 | 66.5 | 73.66 | 4 | 1 | male | 73.5 |
Abaixo temos a dispersão dos dados
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
despine()

Uma forma de capturar a correlação é fazer uma regressão de vizinhos próximos (nearest neighbors). Para tal, precisamos agrupar, no eixo-x, pontos próximos um dos outros. É possível fazer o mesmo nos eixos x e y usando uma distância euclideana. Por simplicidade vamos agrupar apenas em x. No caso particular destes dados onde os valores são bem espalhados no eixo x, podemos simplesmente arredondar os números
#In:
copy = df[['midparentHeight', 'childHeight']].copy()
copy['midparentHeight'] = copy['midparentHeight'].round()
Agrupar por x e tirar a média de y.
#In:
model = copy.groupby('midparentHeight').mean()
model.head()
| childHeight | |
|---|---|
| midparentHeight | |
| 64.0 | 63.000000 |
| 65.0 | 64.229630 |
| 66.0 | 64.350000 |
| 67.0 | 65.535632 |
| 68.0 | 66.240458 |
Observando o modelo.
#In:
x_nn = model.index
y_nn = model.values
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x_nn, y_nn, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
Text(0.5, 1.0, 'Regressão linear simples')

Previsão: Para um novo ponto, arredondar seu peso. Ver valor de y_nn
#In:
idade_media_pais = 71
model.loc[71.0]
childHeight 67.740594
Name: 71.0, dtype: float64
Observe que o modelo acima é muito perto de uma reta. Este é um dos pontos e partidas para entender a correlação linear. Precisamos de alguma forma:
- Capturar a média de valores próximos um dos outros em x
- Capturar a média de valores próximos um dos outros em y
Resolvemos o (1) problema nos dados acima com um round. No caso (2) com um group-by e mean. Observe como o modelo é quase o mesmo quando z-normalizamos os dados.
#In:
znormed = df[['midparentHeight', 'childHeight']].copy()
znormed = (znormed - znormed.mean()) / znormed.std(ddof=1)
znormed.head()
| midparentHeight | childHeight | |
|---|---|---|
| 0 | 3.452802 | 1.803190 |
| 1 | 3.452802 | 0.685637 |
| 2 | 3.452802 | 0.629760 |
| 3 | 3.452802 | 0.629760 |
| 4 | 2.470762 | 1.887006 |
#In:
x = znormed['midparentHeight'].copy()
y = znormed['childHeight'].copy()
#In:
znormed['midparentHeight'] = znormed['midparentHeight'].round()
model = znormed.groupby('midparentHeight').mean()
#In:
x_nn = model.index
y_nn = model.values
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x_nn, y_nn, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
despine()
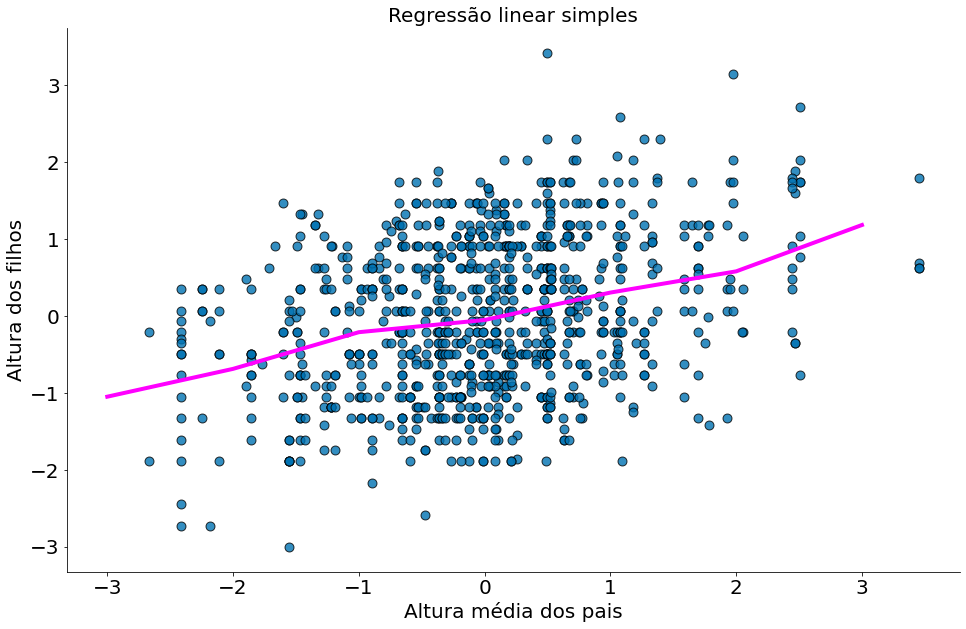
Regressão Linear Simples
Nos slides da aula e no material do , leia a discussão sobre como uma regressão linear tenta capturar a mesma ideia do nosso KNN simples acima. De forma simples, queremos uma reta possível de explicar tando a dispersão em x quanto em y. Tal reta deve se aproximar da média dos dois valores quando vistos em janelas (estilo o NN acima). Em particular, você supõe que existem constantes $\alpha$ (alfa) e $\beta$ (beta) tais que:
\[\hat{y}_i = \beta x_i + \alpha + \epsilon_i\]Idealmente, vamos conseguir capturar o valor médio de $y_i$ para grupos de valores próximos em $x_i$. $\epsilon_i$ é um termo de erro (esperançosamente pequeno) que representa o fato de que existem outros fatores não explicados por este modelo simples.
Como escolhemos alfa e beta? Bem, qualquer escolha de alfa e beta nos dá uma saída prevista para cada entrada $x_i$. Como sabemos a saída real $y_i$, podemos calcular o erro de cada par. Computa o valor $\epsilon_i$.
#In:
def error(alpha, beta, x, y):
model = beta * x + alpha
return y - model
Observe o erro médio para um primeiro modelo
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
alpha = 1
beta = 0.5
e = error(alpha, beta, x, y)
e.mean()
31.142544967880085
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
y_model = beta * x + alpha
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x, y_model, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
Text(0.5, 1.0, 'Regressão linear simples')
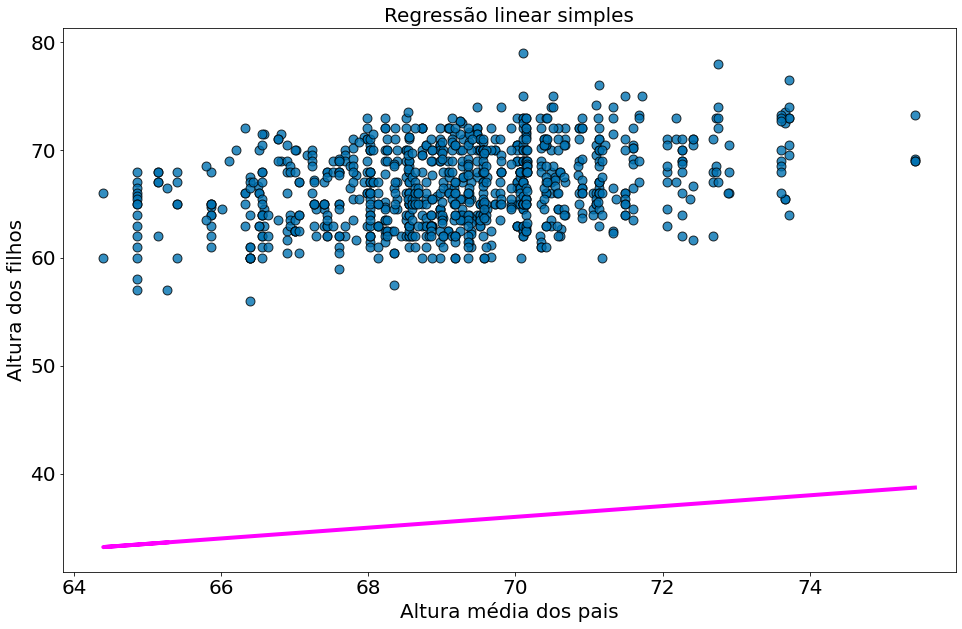
Agora para um segundo.
#In:
alpha = 22
beta = 0.5
e = error(alpha, beta, x, y)
e.mean()
10.142544967880088
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
y_model = beta * x + alpha
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x, y_model, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
Text(0.5, 1.0, 'Regressão linear simples')
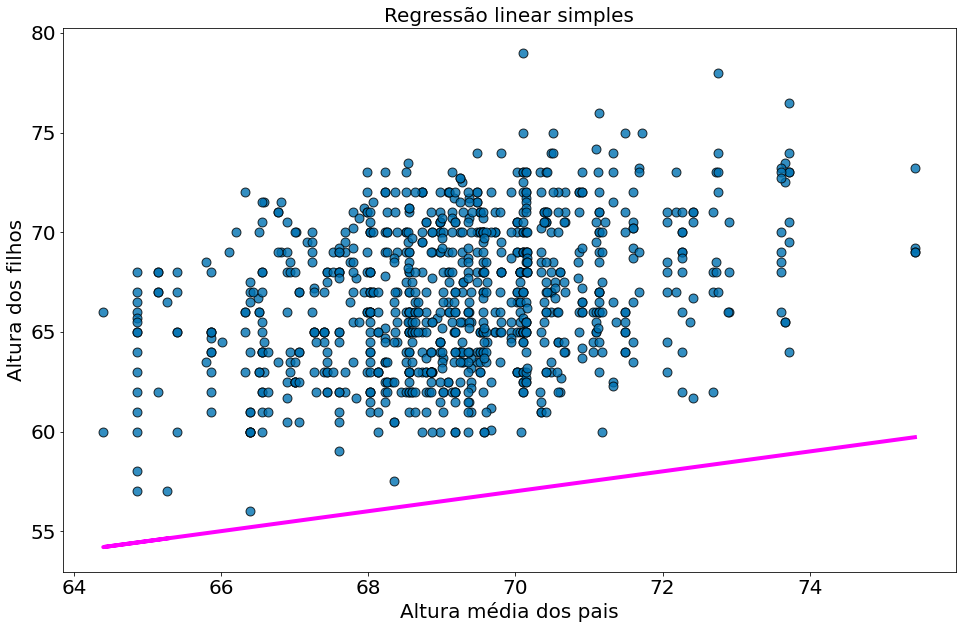
O segundo modelo é bem melhor. Porém os dois são péssimos. Para facilitar a nossa vida, vamos fazer uso da soma dos erros ao quadrado. Isto vai nos ajudar nas derivadas.
Somamos os erros quadrados:
#In:
def sum_of_squared_errors(alpha, beta, x, y):
return (error(alpha, beta, x, y) ** 2).sum()
A solução de mínimos quadrados (least squares solution) é escolher o alfa e o beta que tornam o sum_of_squared_errors o menor possível. Para chegar em tais valores, podemos ver o erro como uma função de $\alpha$, $\beta$. Vamos iniciar com o caso normalizado. Aqui $\alpha=0$.
Dados Normalizados
Lembre-se que na z-normalização, os dados de X e Y ficam com média 0 e desvio 1. Em particular: $x’_i = \frac{x_i - \bar{x}}{s_x}$ e $y’_i = \frac{y_i - \bar{y}}{s_y}$. Note como a média dos dados tanto em X quanto em Y é zero:
\[\bar{x'} = n^{-1} \sum_i \frac{x_i - \bar{x}}{s_x}\] \[\bar{x'} = n^{-1} s^{-1}_x (\sum_i x_i - \bar{x} \sum_i 1)\] \[\bar{x'} = n^{-1} s^{-1}_x (\sum_i x_i - \bar{x} n)\] \[\bar{x'} = n^{-1} s^{-1}_x (\sum_i x_i - x_i)\] \[\bar{x'} = n^{-1} s^{-1}_x (0) = 0\]Além do mais, o desvio padrão é 1. Provando:
\(s_{x'} = n^{-1} \sum_i (\frac{x_i - \bar{x}}{s_x} - 0)^2\) \(s_{x'} = s^{-1}_x n^{-1} \sum_i (x_i - \bar{x})^2\) \(s_{x'} = s^{-1}_x s_x = 1\)
Como a média dos pontos é (0, 0), a nossa melhor reta vai passar pela origem. Ou seja, $\alpha=0$. Além do mais, cada ponto dos seus dados é uma reta entre (0, 0) e o ponto $(x’_i, y’_i)$. Neste caso, resolver o problema abaixo para chegar na equação da reta:
\[L(\beta) = \sum_i (y'_i - \hat{y}'_i)^2\] \[L(\beta) = \sum_i (y'_i - \beta x'_i)^2\] \[L(\beta) = \sum_i y'^2_i - 2 \beta x'_i y'_i + \beta^2 x'^2_i\]Derivando a função em $\beta$:
\[\frac{d}{d\beta} L(\Theta) = -\sum_i 2 x'_i y'_i + 2 \beta x'^2_i\]Fazendo $\frac{d}{d\beta}=0$:
\[\beta = \frac{\sum_i x'_i y'_i}{x'^2_i}\]Nos slides discutimos como tal solução captura é uma função da covariância dos dados.
Dados Originais
Agora vamos resolver sem normalizar os dados. Vamos definir $\Theta = [\alpha, \beta]$, isto é, um vetor com alfa e beta.
\[L(\Theta) = \sum_i (y_i - \hat{y}_i)^2\] \[L(\Theta) = \sum_i (y_i - \beta x_i + \alpha)^2\]Resolvendo o quadrado dentro do somatório temos:
\[L(\Theta) = \sum_i (y_i^2 + \alpha^2 + x_i^2\beta^2 - 2 \beta \alpha x_i - 2 \beta x_i y_i + 2\alpha y_i)\]Derivando em relação a $\alpha$:
\[\frac{d}{d\alpha} L(\Theta)= \sum_i (2\alpha - 2 \beta x_i + 2\beta y_i)\]Derivando em relação a $\beta$:
\[\frac{d}{d\beta} L(\Theta) = \sum_i (2x_i^2\beta - 2 \alpha x_i + 2 x_i y_i)\]Para resolver otimizar esta função precisamos setar as duas derivadas para zero.
\[\frac{d}{d\alpha} L(\Theta) = 0\] \[\frac{d}{d\beta} L(\Theta) = 0\]Após isto, podemos resolver os valores ótimos de $\alpha$ e $\beta$. Note que esta é uma otimização um pouco chata de resolve.
\begin{align} \alpha & = \bar{y} - \beta\,\bar{x}, \[5pt] \beta &= \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) }{ \sum_{i=1}^n (x_i - \bar{x})^2 } \[6pt] &= \frac{ \operatorname{Cov}(x, y) }{ \operatorname{Var}(x) } \[5pt] &= r_{xy} \frac{s_y}{s_x}. \[6pt] \end{align}
#In:
def least_squares_fit(x, y):
correlationxy = ss.pearsonr(x, y)[0]
beta = correlationxy * np.std(y, ddof=1) / np.std(x, ddof=1)
alpha = np.mean(y) - beta * np.mean(x)
return alpha, beta
Sem passar pela matemática exata, vamos pensar em por que isso pode ser uma solução razoável. A escolha do alfa simplesmente diz que quando vemos o valor médio da variável independente $x$, predizemos o valor médio da variável dependente $y$.
A escolha de beta significa que quando o valor de entrada aumenta pelo desvio padrão de $x$, a previsão de $y$ aumenta pela correlação entre $x$ e $y$ multiplicada pelo desvio padrão de $y$ (correlationxy * np.std(y)). No caso em que $x$ e $y$ estão perfeitamente correlacionados, um aumento de um desvio padrão em $x$ resulta em um aumento de um desvio padrão de $y$ na predição. Quando eles são perfeitamente anti-correlacionados, o aumento em $x$ resulta em uma diminuição no valor da previsão. E quando a correlação é zero, o beta é zero, o que significa que as alterações em $x$ não afetam a previsão.
Para um pouco mais sobre a intuição dessa fórmula, veja este vídeo.
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
alpha, beta = least_squares_fit(x, y)
y_model = beta * x + alpha
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x, y_model, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
Text(0.5, 1.0, 'Regressão linear simples')
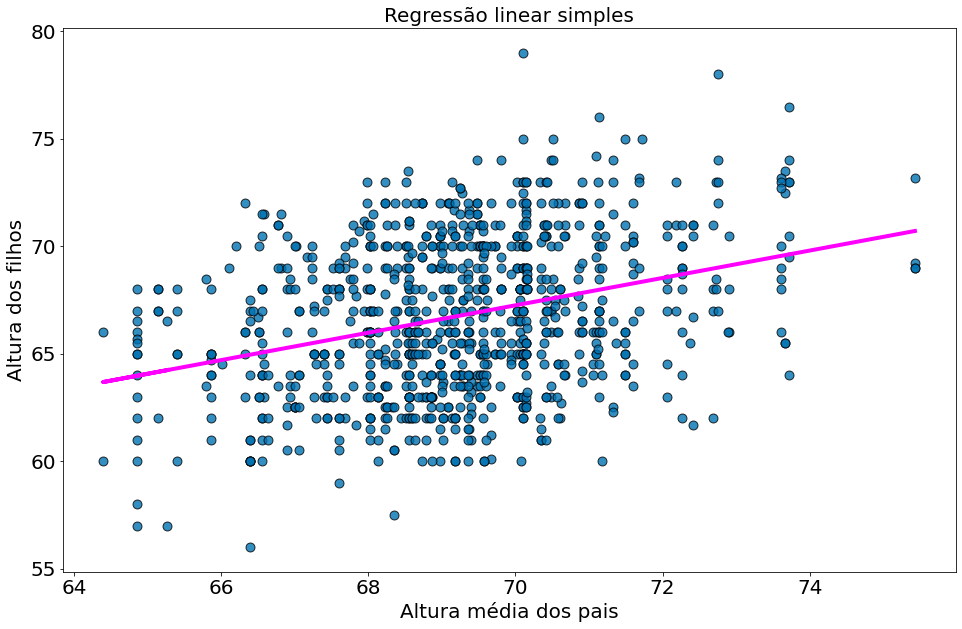
#In:
alpha, beta
(22.636240549589736, 0.6373608969694791)
Isso fornece valores de alfa = 22,63 e beta = 0,63. Portanto, podemos dizer que crianças vão ser aproximadamente 22 polegadas maiores do que a 63\% da média da altura dos seus pais.
É claro que precisamos de uma maneira melhor de descobrir o quão bem nós ajustamos os dados do que simplesmente encarar o gráfico da regressão. Uma medida comum é o coeficiente de determinação (ou R-quadrado, ou $R^2$, ou R-dois), que mede a fração da variação total na variável dependente (o $y$) que é capturada pelo modelo:
#In:
def total_sum_of_squares(y):
return ((y - y.mean()) ** 2).sum()
def r_squared(alpha, beta, x, y):
return 1.0 - (sum_of_squared_errors(alpha, beta, x, y) /
total_sum_of_squares(y))
#In:
r_squared(alpha, beta, x, y)
0.10300883578346631
Agora, escolhemos o alfa e o beta que minimizaram a soma dos quadrados dos erros de previsão. Um modelo linear que poderíamos ter escolhido é “sempre prever a média de $y$” (correspondendo a alpha = np.mean(y) e beta = 0), cuja soma dos erros quadrados é exatamente igual a sua soma total de quadrados. Isso significa um $R^2$ de zero, que indica um modelo que (obviamente, neste caso) não funciona melhor do que apenas prever a média.
Claramente, o modelo de mínimos quadrados deve ser pelo menos tão bom quanto esse, o que significa que a soma dos erros quadrados é no máximo a soma total de quadrados, o que significa que o $R^2$ deve ser pelo menos zero. E a soma dos erros quadrados deve ser pelo menos $0$, o que significa que o $R^2$ pode ser no máximo $1$.
Quanto maior for o $R^2$, melhor o nosso modelo se ajusta aos dados. Aqui nós calculamos um $R^2$ de $0.10$, o que nos diz que o nosso modelo está fraco ajustar os dados, e que claramente existem outros fatores em jogo.
Observe como o modelo para, visualmente, bem pior ao plotar em outra escala. Existe muita variabilidade no eixo-y para ser capturada.
#In:
x = df['midparentHeight'].values
y = df['childHeight'].values
alpha, beta = least_squares_fit(x, y)
y_model = beta * x + alpha
plt.scatter(x, y, alpha=0.8, edgecolors='k', s=80)
plt.plot(x, y_model, color='magenta')
plt.xlabel('Altura média dos pais')
plt.ylabel('Altura dos filhos')
plt.title('Regressão linear simples')
plt.xlim((55, 80))
plt.ylim((55, 80))
(55.0, 80.0)
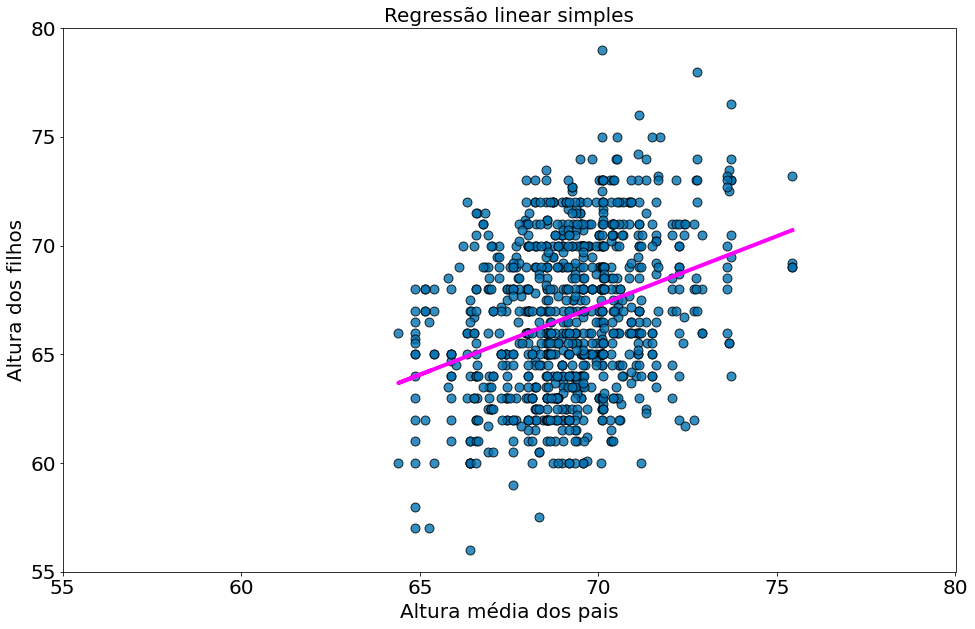
Por fim, a raiz de $R^2$ é a correlação.
#In:
r_squared(alpha, beta, x, y) ** 0.5
0.32094989606395935
#In:
ss.pearsonr(x, y)[0]
0.3209498960639593
Formas de interpretar o $R^2$.
- Quão melhor é o meu modelo de um que retorna apenas a média de y.
- Quanto da variancia de y é explicada por x. Apenas 10% acima.
Para entender o segundo ponto, o total_sum_of_squares é proporcional a variância. Na verdade é $s_y$ * (n-1). Ou seja, sem tirar a média dos desvios quadrados. Sendo $\hat{y}_i$ a nossa previsão.
$(y_i - \bar{y})^2$ define nossa variância. Quanto dela está em $(y_i - \hat{y}_i)^2$. Esta é outra forma de pensar no $R^2$.
Bootstrap na Regressão
Lembre-se que nossa regressão foi realizada em uma amostra. Portanto, qualque estatística que temos vêm com erros. Os coeficientes da nossa regressão: $\alpha$ e $\beta$ têm erros. Além da correlação $r$ e do $R^2$. Como saber a variablidade de tais estimativas? Bootstrap. O código abaixo faz um Bootstrap de: $\alpha$, $\beta$ e $R^2$.
#In:
def bootstrap_regression(df, n=10000, size=None):
if size is None:
size = len(df)
alphas = np.zeros(n)
betas = np.zeros(n)
rs = np.zeros(n)
for i in range(n):
sample = df.sample(size, replace=True)
x = sample['midparentHeight'].values
y = sample['childHeight'].values
alpha, beta = least_squares_fit(x, y)
alphas[i] = alpha
betas[i] = beta
rs[i] = ss.pearsonr(x, y)[0] ** 2
return alphas, betas, rs
#In:
alphas, betas, rs = bootstrap_regression(df)
Plotando para alfa
#In:
plt.hist(alphas, edgecolor='k')
lower = np.percentile(alphas, 2.5)
upper = np.percentile(alphas, 97.5)
despine()
print(alphas.mean())
print(lower, upper)
22.633892839512196
14.607617132670345 30.700075002921505
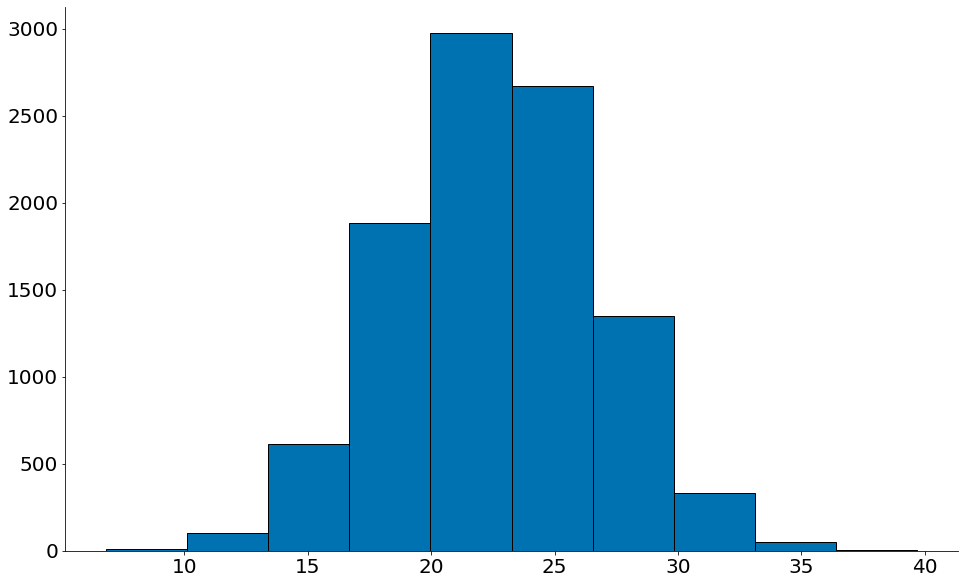
Beta
#In:
plt.hist(betas, edgecolor='k')
lower = np.percentile(betas, 2.5)
upper = np.percentile(betas, 95)
despine()
print(betas.mean())
print(lower, upper)
0.6374269876165028
0.5211173140252211 0.735220236941085
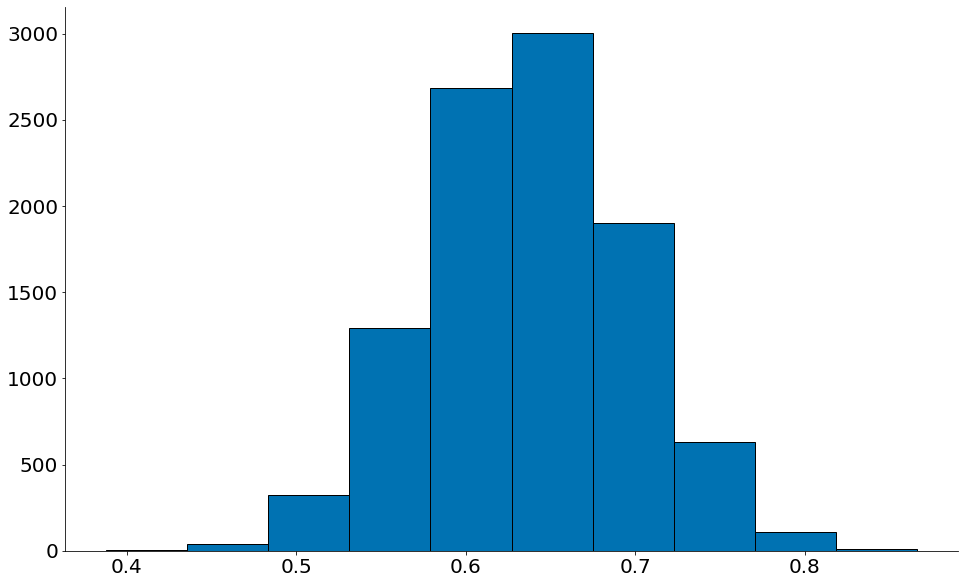
R2
#In:
plt.hist(rs, edgecolor='k')
lower = np.percentile(rs, 2.5)
upper = np.percentile(rs, 97.5)
despine()
print(rs.mean())
print(lower, upper)
0.1036488020412463
0.06988925762152452 0.140625175103405
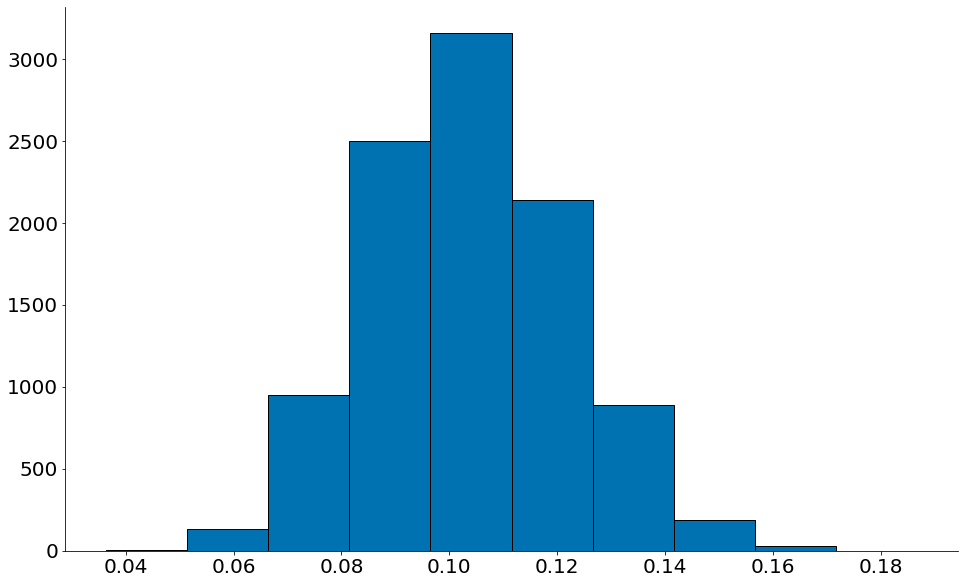
Statsmodels
Observe como entender tal ideia é interessante. Quanto usamos bibliotecas mais avançadas, tipo o statsmodels, os resultados descrevem: ICs para cada parâmetro e valores-p. No notebook anterior computamos um valor-p da correlação com permutação. Podemos fazer o mesmo para alfa e beta. Classicamente, existem estatísticas para tais valores como a $F$ measure que permitem ics e valores-p teóricos.
#In:
import statsmodels.api as sm
stocks = {'Year': [2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016],
'Month': [12, 11,10,9,8,7,6,5,4,3,2,1,12,11,10,9,8,7,6,5,4,3,2,1],
'Interest_Rate': [2.75,2.5,2.5,2.5,2.5,2.5,2.5,2.25,2.25,2.25,2,2,2,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75],
'Unemployment_Rate': [5.3,5.3,5.3,5.3,5.4,5.6,5.5,5.5,5.5,5.6,5.7,5.9,6,5.9,5.8,6.1,6.2,6.1,6.1,6.1,5.9,6.2,6.2,6.1],
'Stock_Index_Price': [1464,1394,1357,1293,1256,1254,1234,1195,1159,1167,1130,1075,1047,965,943,958,971,949,884,866,876,822,704,719]
}
df = pd.DataFrame(stocks, columns=['Year','Month', 'Interest_Rate', 'Unemployment_Rate', 'Stock_Index_Price'])
Oberver o IC da constante (alfa) abaixo. Note que a mesma não é siginificativa. Como o IC abrange números negativos e positivos, não podemos descartar um zero como sendo a média.
#In:
X = df['Interest_Rate']
Y = df['Stock_Index_Price']
X = sm.add_constant(X) # adding a constant
model = sm.OLS(Y, X).fit()
predictions = model.predict(X)
print_model = model.summary()
print(print_model)
OLS Regression Results
==============================================================================
Dep. Variable: Stock_Index_Price R-squared: 0.876
Model: OLS Adj. R-squared: 0.870
Method: Least Squares F-statistic: 155.0
Date: Wed, 03 Feb 2021 Prob (F-statistic): 1.95e-11
Time: 18:12:17 Log-Likelihood: -136.94
No. Observations: 24 AIC: 277.9
Df Residuals: 22 BIC: 280.2
Df Model: 1
Covariance Type: nonrobust
=================================================================================
coef std err t P>|t| [0.025 0.975]
---------------------------------------------------------------------------------
const -99.4643 95.210 -1.045 0.308 -296.918 97.990
Interest_Rate 564.2039 45.317 12.450 0.000 470.221 658.186
==============================================================================
Omnibus: 5.361 Durbin-Watson: 0.514
Prob(Omnibus): 0.069 Jarque-Bera (JB): 3.647
Skew: -0.927 Prob(JB): 0.161
Kurtosis: 3.459 Cond. No. 15.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.