Testes AB
Como comparar dois grupos
Resultados Esperados
- Comparar dois grupos usando intervalos de confiança
- Entender como fazer um comparativo de dois grupos
- Fazer uso do Bootstrap para comparar grupos
- Fazer uso de ICs para comparar grupos
Sumário
#In:
# -*- coding: utf8
from scipy import stats as ss
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (12, 8)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Partes da discussão vem do material do Professor Nazareno Andrade
Neste notebook vamos continuar nossa exploração de intervalos de confiança e o significado dos mesmos. Em particular, vamos continuar também usando o bootstrap para entender o conceito. Lembre-se que a ideia de um intervalo de confiança é entender a média da população com base em uma amostra. Por isso o teorema central do limite é tão importante. Na aula anterior iniciamos assumindo que conhecíamos a população. Quando isso ocorre tudo é muito mais simples, quase nunca é verdade. Então como falar algo da população usando apenas uma amostra?
Perguntas como esta acima são a base da estatística frequentista. Assumimos que uma verdade existe, na população, e queremos saber como entender essa população só com uma amostra.
Para este notebook, preparei algumas funções abaixo que computa.
- IC da média usando o TCL
- IC da média usando bootstrap
- IC da diferença entre duas médias usando bootstrap
Funções abaixo com documentação
#In:
def bootstrap_mean(df, column, n=5000, size=None):
'''
Faz um boostrap da média. Gera amostras.
Parâmetros
----------
df: o dataframe
column: a coluna que queremos focar
n: número de amostras para o bootstrap
size: tamanho de cada amostra, por padrão vira o tamanho do df.
'''
if size is None:
size = len(df)
values = np.zeros(n)
for i in range(n):
sample = df[column].sample(size, replace=True)
values[i] = sample.mean()
return values
#In:
def ic_bootstrap(df, column, n=5000, size=None):
'''
Faz um IC boostrap da média. Gera um Intervalo.
Parâmetros
----------
df: o dataframe
column: a coluna que queremos focar
n: número de amostras para o bootstrap
size: tamanho de cada amostra, por padrão vira o tamanho do df.
'''
values = bootstrap_mean(df, column, n, size)
return (np.percentile(values, 2.5), np.percentile(values, 97.5))
#In:
def ic_classic(df, column):
'''
Faz um IC clássico usando o teorema central do limite.
Parâmetros
----------
df: o dataframe
column: a coluna que queremos focar
n: número de amostras para o bootstrap
size: tamanho de cada amostra, por padrão vira o tamanho do df.
'''
data = df[column]
mean = data.mean()
std = data.std(ddof=1)
se = std / np.sqrt(len(data))
return (mean - 1.96 * se, mean + 1.96 * se)
Entendimento Inicial com Dados Sintéticos
Vamos, mais uma vez entender um IC usando o bootstrap. Inicialmente, vamos assumir uma população $Normal(0, 1)$. Obviamente, teremos média perto de = 0 e std = 1.
Caso queira, brinque com o size acima e observe como a média fica mais correta. Além do mais, códigos scipy usam dois parâmetros: loc e scale. LEIA ATENTAMENTE A DOCUMENTAÇÃO ANTES DE USAR AS DISTRIBUIÇÕES. ÀS VEZES, LOC e SCALE MAPEAM DIRETAMENTE PARA O UM LIVRO/WIKIPEDIA. NO CASO DA NORMAL BATE.
Sobre Scipy. Leia o link abaixo para entender a API um pouco mais. https://www.johndcook.com/blog/distributions_scipy/
#In:
pop = ss.distributions.norm.rvs(size=10000, loc=0, scale=1)
#In:
pop.mean()
-0.003189792945110248
#In:
pop.std(ddof=1)
0.9998611935142725
Vou converter os dados para um DataFrame. Além do mais, vou comparar o IC do bootstrap com o IC real ao variar o número de amostras no meu Bootstrap.
#In:
pop = ss.distributions.norm.rvs(size=100, loc=0, scale=1)
data = pd.DataFrame()
data['values'] = pop
serie_1 = []
serie_2 = []
ns = np.arange(1, 1001)
for n in ns:
ic_bs = ic_bootstrap(data, 'values', n=n)
ic_c = ic_classic(data, 'values')
tamanho_bs = ic_bs[1] - ic_bs[0]
tamanho_c = ic_c[1] - ic_c[0]
serie_1.append(tamanho_bs)
serie_2.append(tamanho_c)
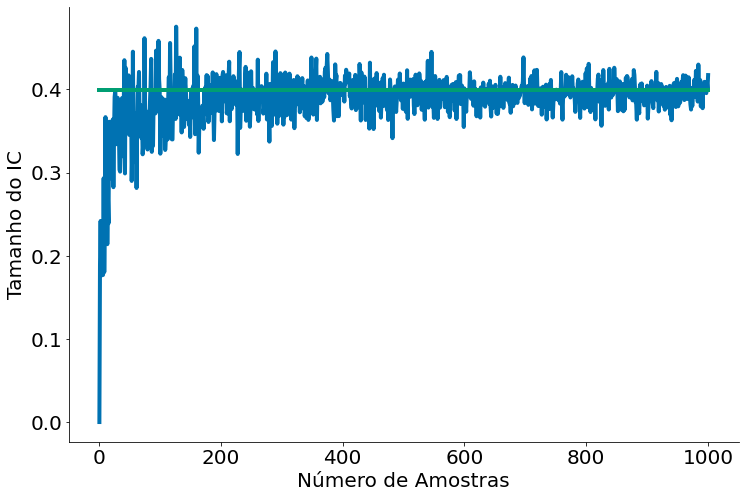
No gráfico abaixo note que como o IC com bootstrap vai cada vez mais parecendo com o IC clássico (com SE/erro padrão). Ou seja, os dois estimam o mesmo intervalo. O gráfico mostra o tamanho do intervalo, mas já discutimos como o valor do intervalo é similar.
#In:
plt.plot(ns, serie_1, label='Bootstrap')
plt.plot(ns, serie_2, label='Real')
plt.xlabel('Número de Amostras')
plt.ylabel('Tamanho do IC')
despine()
Dados Reais
Agora vamos explorar dados reais para entender se existe algum efeito entre fumar o peso.
Algumas hipóteses
Tente brincar com os dados para entender um pouco mais cada caso.
- Mães que fumam tendem a ter bebês com pesos menores.
- Mães que têm idade menor tendem a ter bebês com pesos menores.
- Mães que têm peso menor tendem a ter bebês com pesos menores.
Vamos explorar a primeira.
Primeiro, vamos dar uma olhada na base como um todo.
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/10-AB/baby.csv')
# Convertendo para unidades não EUA
df['Birth Weight'] = 0.0283495 * df['Birth Weight']
df['Maternal Pregnancy Weight'] = 0.0283495 * df['Maternal Pregnancy Weight']
df['Maternal Height'] = 0.0254 * df['Maternal Height']
df.head()
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | Maternal Smoker | |
|---|---|---|---|---|---|---|
| 0 | 3.401940 | 284 | 27 | 1.5748 | 2.834950 | False |
| 1 | 3.203493 | 282 | 33 | 1.6256 | 3.827183 | False |
| 2 | 3.628736 | 279 | 28 | 1.6256 | 3.260193 | True |
| 3 | 3.061746 | 282 | 23 | 1.7018 | 3.543687 | True |
| 4 | 3.855532 | 286 | 25 | 1.5748 | 2.636503 | False |
#In:
df.describe()
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | |
|---|---|---|---|---|---|
| count | 1174.000000 | 1174.000000 | 1174.000000 | 1174.000000 | 1174.000000 |
| mean | 3.386703 | 279.101363 | 27.228279 | 1.626855 | 3.642307 |
| std | 0.519609 | 16.010305 | 5.817839 | 0.064163 | 0.587807 |
| min | 1.559222 | 148.000000 | 15.000000 | 1.346200 | 2.466407 |
| 25% | 3.061746 | 272.000000 | 23.000000 | 1.574800 | 3.238930 |
| 50% | 3.401940 | 280.000000 | 26.000000 | 1.625600 | 3.543687 |
| 75% | 3.713785 | 288.000000 | 31.000000 | 1.676400 | 3.940580 |
| max | 4.989512 | 353.000000 | 45.000000 | 1.828800 | 7.087375 |
Agora vamos ver os dados de quem fuma.
#In:
smokers = df[df['Maternal Smoker'] == True]
smokers.describe()
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | |
|---|---|---|---|---|---|
| count | 459.000000 | 459.000000 | 459.000000 | 459.000000 | 459.000000 |
| mean | 3.226717 | 277.897603 | 26.736383 | 1.628256 | 3.598101 |
| std | 0.518654 | 15.201427 | 5.713139 | 0.066135 | 0.566761 |
| min | 1.644271 | 223.000000 | 15.000000 | 1.346200 | 2.466407 |
| 25% | 2.863300 | 271.000000 | 22.000000 | 1.587500 | 3.175144 |
| 50% | 3.260193 | 278.000000 | 26.000000 | 1.625600 | 3.543687 |
| 75% | 3.572037 | 286.000000 | 30.000000 | 1.676400 | 3.869707 |
| max | 4.620969 | 330.000000 | 43.000000 | 1.828800 | 6.095142 |
Contra os dados de quem não fuma.
#In:
no_smokers = df[df['Maternal Smoker'] == False]
no_smokers.describe()
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | |
|---|---|---|---|---|---|
| count | 715.000000 | 715.000000 | 715.000000 | 715.000000 | 715.000000 |
| mean | 3.489407 | 279.874126 | 27.544056 | 1.625955 | 3.670685 |
| std | 0.493953 | 16.472823 | 5.866317 | 0.062895 | 0.599603 |
| min | 1.559222 | 148.000000 | 17.000000 | 1.422400 | 2.523105 |
| 25% | 3.203493 | 273.000000 | 23.000000 | 1.574800 | 3.260193 |
| 50% | 3.486988 | 281.000000 | 27.000000 | 1.625600 | 3.572037 |
| 75% | 3.798833 | 289.000000 | 31.000000 | 1.676400 | 3.968930 |
| max | 4.989512 | 353.000000 | 45.000000 | 1.803400 | 7.087375 |
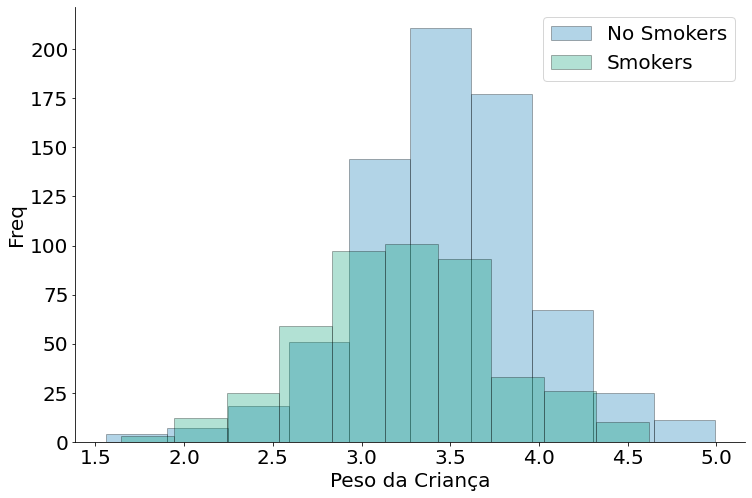
Oberserve que sim, existem diferenças nos valores. Porém precisamos de um arcabouço para entender exatamente como comparar os grupos. Não é impossível que tais erros sejam factíveis em uma amostra. Até na distribuição temos diferença, mas podemos fazer alguma coisa mais fundamentada (com garantias estatísticas) com uma amostra?!
#In:
plt.hist(no_smokers['Birth Weight'], alpha=0.3, edgecolor='k', label='No Smokers')
plt.hist(smokers['Birth Weight'], alpha=0.3, edgecolor='k', label='Smokers')
despine()
plt.xlabel('Peso da Criança')
plt.ylabel('Freq')
plt.legend()
<matplotlib.legend.Legend at 0x7efda8347dc0>
Por isso que ICs são bem interessante. Vemos qual a chance do parâmetro na população, depois comparamos os ICs.
Abaixo temos o IC de cada caso com bootstrap. Podemos falar alguma coisa?!
#In:
ic_bootstrap(smokers, 'Birth Weight')
(3.18088801633987, 3.2741541655228756)
#In:
ic_bootstrap(no_smokers, 'Birth Weight')
(3.452928459108392, 3.526363576520979)
#In:
samples_smokers = bootstrap_mean(smokers, 'Birth Weight')
samples_no_smokers = bootstrap_mean(no_smokers, 'Birth Weight')
to_plot = pd.DataFrame()
to_plot['smoker_boot'] = samples_smokers
to_plot['no_smoker_boot'] = samples_no_smokers
#In:
to_plot.boxplot(grid=False, sym='', whis=[5, 95], showmeans=True)
plt.ylim(3, 3.6)
plt.ylabel('Media')
despine()
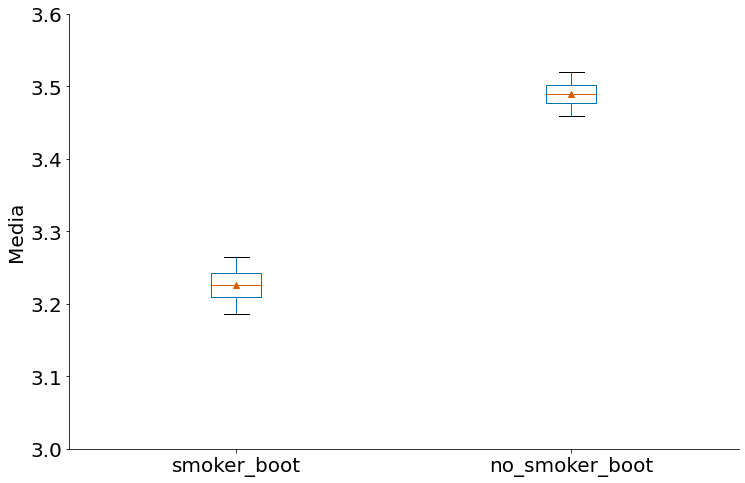
Uma forma mais simples de entender é comparar a diferença entre os dois grupos. Note que o bootstrap também pode ser utilizado, agora vamos comparar a média de cada amostra. É o mesmo arcabouço.
#In:
def bootstrap_diff(df1, df2, column, n=5000, size=None):
'''
Faz um boostrap da diferença das média. Gera amostras.
Parâmetros
----------
df: o dataframe
column: a coluna que queremos focar
n: número de amostras para o bootstrap
size: tamanho de cada amostra, por padrão vira o tamanho do df.
'''
if size is None:
size = len(df)
values = np.zeros(n)
for i in range(n):
sample1 = df1[column].sample(size, replace=True)
sample2 = df2[column].sample(size, replace=True)
values[i] = sample1.mean() - sample2.mean()
return values
#In:
caso2 = pd.DataFrame()
diff = bootstrap_diff(smokers, no_smokers, 'Birth Weight')
#In:
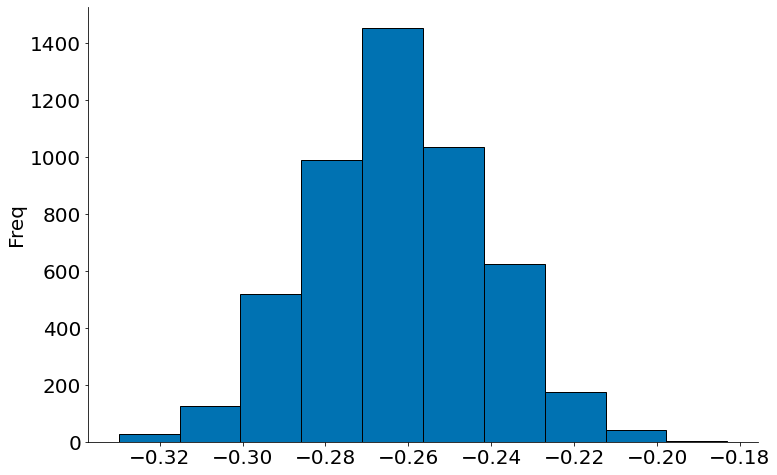
plt.hist(diff, edgecolor='k')
plt.ylabel('Média Fumantes - Não Fumantes')
plt.ylabel('Freq')
despine()
#In:
from statsmodels.distributions.empirical_distribution import ECDF
ecdf = ECDF(diff)
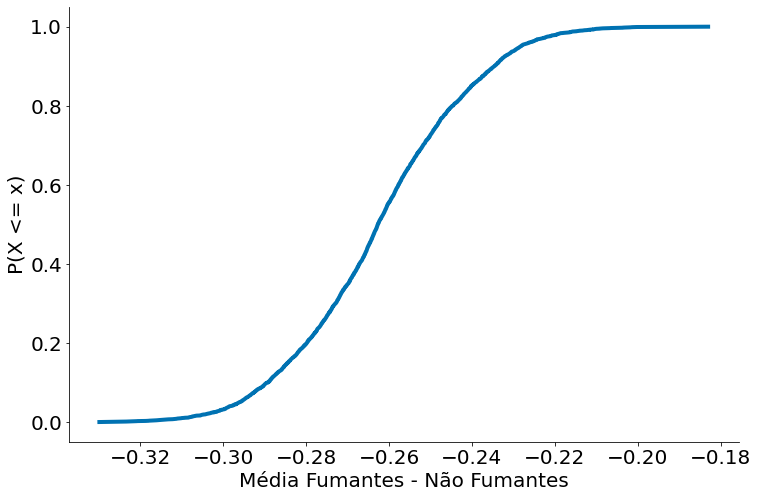
plt.plot(ecdf.x, ecdf.y)
plt.xlabel('Média Fumantes - Não Fumantes')
plt.ylabel('P(X <= x)')
despine()