Intervalos de Confiança
Conceito base para pesquisas estatísticas
Resultados Esperados
- Entender como a distribuição amostral faz inferência
- Uso e entendimento de ICs através do teorema central do limite
- Uso e entendimento de ICs através do bootstrap
- Como os dois se ligam
Sumário
- Introdução
- Distribuição amostral e Intervalos de Confiança
- Exemplo Moedas (Caso onde Sabemos da População!)
- Simulando
- Quando não sabemos de muita coisa
- ICs com Normal
- Computando um IC dos dados
- Entendendo um IC
- A situação mais comum na vida real
- Brincando com o bootstrap
- Comparando o Bootstrap com o caso Teórico
#In:
# -*- coding: utf8
from IPython.display import HTML
from matplotlib import animation
from scipy import stats as ss
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
/tmp/ipykernel_15850/1539025901.py:1: MatplotlibDeprecationWarning: The seaborn styles shipped by Matplotlib are deprecated since 3.6, as they no longer correspond to the styles shipped by seaborn. However, they will remain available as 'seaborn-v0_8-<style>'. Alternatively, directly use the seaborn API instead.
plt.style.use('seaborn-colorblind')
#In:
plt.ion()
<contextlib.ExitStack at 0x7f48e83c0050>
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Vamos explorar a ideia de intervalos de confiança. Inicialmente, lembre-se do teorema central do limite que diz: se $X_1, …, X_n$ são variáveis aleatórias. Em particular, todas as VAs foram amostradas de uma mesma população com média $\mu$ (finita), desvio padrão $\sigma$ (finito). Além do mais, a geração de cada VA é independente da outra, sendo toas identicamente distribuídas. Quando $n$ é grande, então
\[\frac{1}{n}(X_1 + \cdots + X_n)\]é aproximadamente distribuído por uma Normal com média $\mu$ e desvio padrão $\sigma/\sqrt{n}$:
\(\frac{1}{n}(X_1 + \cdots + X_n) \sim Normal(\mu, \sigma/\sqrt{n})\).
Distribuição amostral e Intervalos de Confiança
A distribuição dos valores de uma estatística a partir de amostras é chamada de distribuição amostral daquela estatística. Ela tem um papel importante, porque é a partir do entendimento dela que estimaremos quanta confiança temos em uma estatística que estamos calculando a partir de uma amostra. No exemplo acima, cada $X_i$ é uma amostra e $X_i/n$ é a média desta amostra. Então, $\frac{1}{n}(X_1 + \cdots + X_n)$ é a distribuição amostral das médias!
O principal a entender aqui é que se conhecermos a distribuição amostral, saberemos quão longe normalmente a estatística calculada para uma amostra está daquela calculada para a população. Sabendo isso, podemos calcular uma margem de erro para a estimativa feita a partir da amostra, tal estimativa será o nosso intervalo de confiança.
Vamos iniciar com um caso que conheçemos a distribuição da população.
Exemplo Moedas (Caso onde Sabemos da População!)
É importante falar que por um bom tempo este notebook não vai computar ICs, preste atenção no fluxo de ideias.
Por simplicidade, vamos fazer uso um exemplo de lançamento de moedas. Isto é, vamos explorar a probabilidade de uma moeda ser justa usando estatística e amostragem (conceitos não exclusivos).
Lembrando, temos um espaço amostral:
\begin{align} \mathcal{S} &= {h, t}
P(h) &= 0.5
P(t) &= 0.5 \end{align}
No caso das moedas é simples saber a distribuição da população. O número de sucessos de lançamentos de uma moeda segue uma distribuição Binomial. A mesma se parece bastante com a Normal. A PMF de uma Binomial é:
\[P(k; p, n) = \binom{n}{k} p^k (1-p)^{n-k}\]onde $n$ captura o número de caras e $k$ o número de lançamentos.
#In:
p = 0.5 # probabilidade de heads/tails
k = 30 # temos 30 jogadas
x = np.arange(0, 31) # Valores no eixo x
prob_binom = ss.distributions.binom.pmf(x, k, p)
plt.stem(x, prob_binom)
plt.xlabel('Num Caras - x')
plt.ylabel('P(sair x caras)')
despine()

Usando a função ppf podemos ver onde ficam $95\%$ dos lançamentos de moedas. Para isto, temos que considerar $2.5\%$ para a esquerda e $2.5\%$ para a direita.
A ppf pode é inverso da CDF. Pegamos valor no percentil, não o percentil dado um valor.
#In:
p = 0.5 # probabilidade de heads/tails
k = 30 # temos 30 jogadas
x = np.arange(0, 31) # Valores no eixo x
prob_binom = ss.distributions.binom.cdf(x, k, p)
plt.step(x, prob_binom)
plt.xlabel('Num Caras - x')
plt.ylabel('P(X <= x)')
plt.title('CDF da Binomial')
despine()

#In:
# 2.5% dos dados P[X <= 10] = 0.025
ss.distributions.binom.ppf(0.025, k, p)
10.0
#In:
print(1-0.025)
# 2.5% dos dados para cima P[X > 20] = 0.025
ss.distributions.binom.ppf(1-0.025, k, p)
0.975
20.0
Caso 1: Quando sabemos a população é fácil responder a pergunta
$95\%$ dos lançamentos de 30 moedas justas deve cair entre 10 e 20. Acamos de computar lá em cima usando o inverso da CDF a PPF.
#In:
p = 0.5 # probabilidade de heads/tails
k = 30 # temos 30 jogadas
x = np.arange(0, 31) # Valores no eixo x
prob_binom = ss.distributions.binom.pmf(x, k, p)
plt.stem(x, prob_binom)
plt.xlabel('Num Caras - x')
plt.ylabel('P(sair x caras)')
despine()
x2 = np.arange(10, 21) # Valores no eixo x
prob_binom = ss.distributions.binom.pmf(x2, k, p)
plt.fill_between(x2, prob_binom, color='r', alpha=0.5)
<matplotlib.collections.PolyCollection at 0x7f49380544d0>

Simulando
Agora, vamos assumir que não sei disto. Isto é, não sei nada de ppf, pdf, pmf, cdf etc. Mas eu sei jogar moedas para cima. Será que consigo estimar o mesmo efeito?!
#In:
# Jogando uma única moeda
np.random.randint(0, 2)
1
#In:
# Jogando 30 moedas
np.random.randint(0, 2, size=30)
array([0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0,
0, 1, 1, 0, 1, 1, 1, 0])
#In:
NUM_SIMULACOES = 100000
resultados = []
for i in range(NUM_SIMULACOES):
jogadas = np.random.randint(0, 2, size=30) # joga 30 moedas para cima
n_caras = (jogadas == 1).sum() # conta quantas foram == 1, caras
resultados.append(n_caras)
bins = np.arange(0, 31) + 0.5
plt.hist(resultados, bins=bins, edgecolor='k');
despine()
plt.xlabel('Numero de Caras')
plt.ylabel('Fração de Casos')
Text(0, 0.5, 'Fração de Casos')
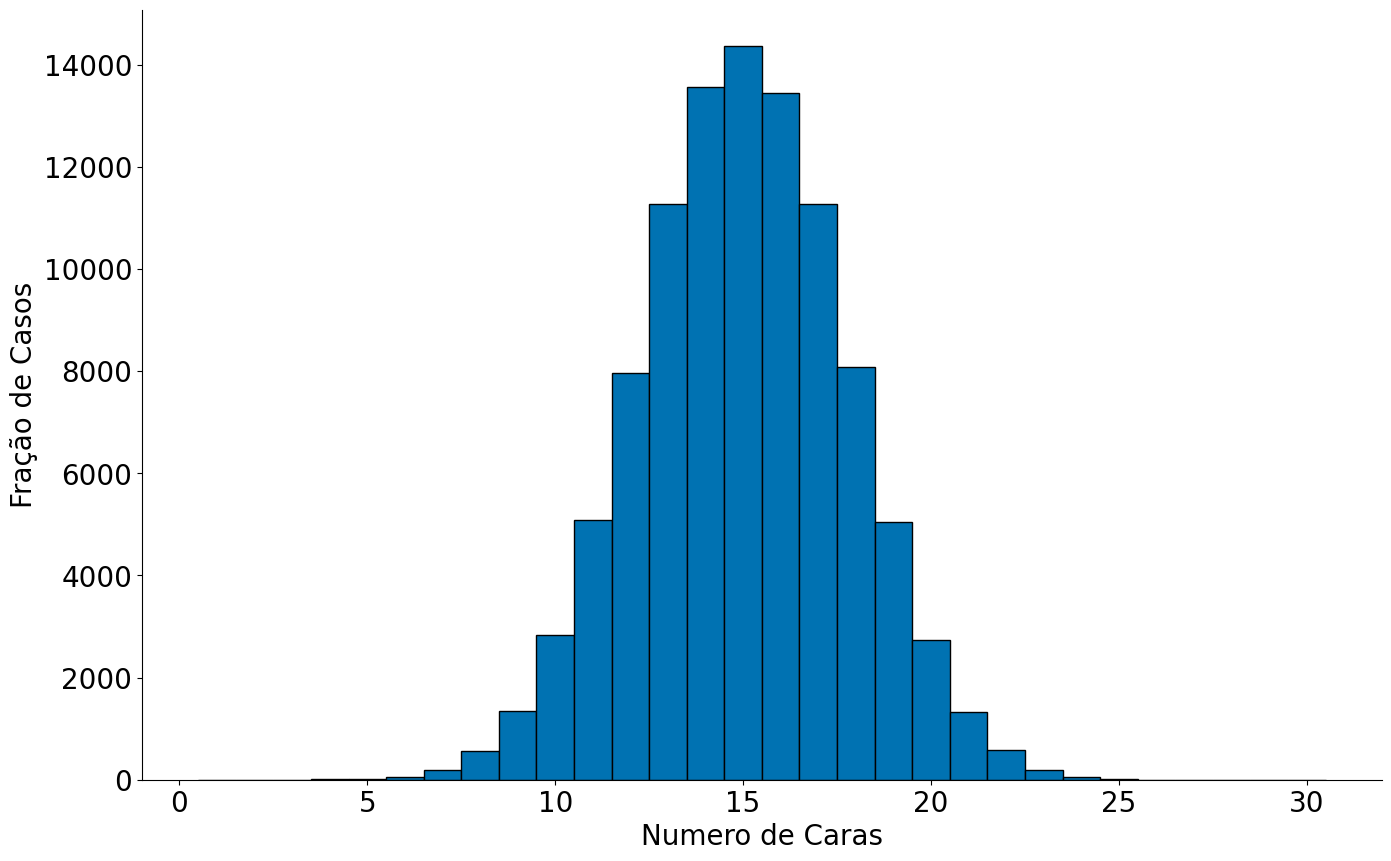
Caso 2: Quando sabemos gerar dados que seguem a população é fácil responder a pergunta.
Podemos verificar o resultado empiricamente na CDF. Estou usando side='left' pois por motivos que não entendo o statsmodels faz P[X < x] e não P[X <= x] por default. Com side left corrigimos isto.
#In:
from statsmodels.distributions.empirical_distribution import ECDF
ecdf = ECDF(resultados, side='left')
plt.plot(ecdf.x, ecdf.y)
plt.xlabel('Num caras')
plt.ylabel('P[X <= x]')
despine()
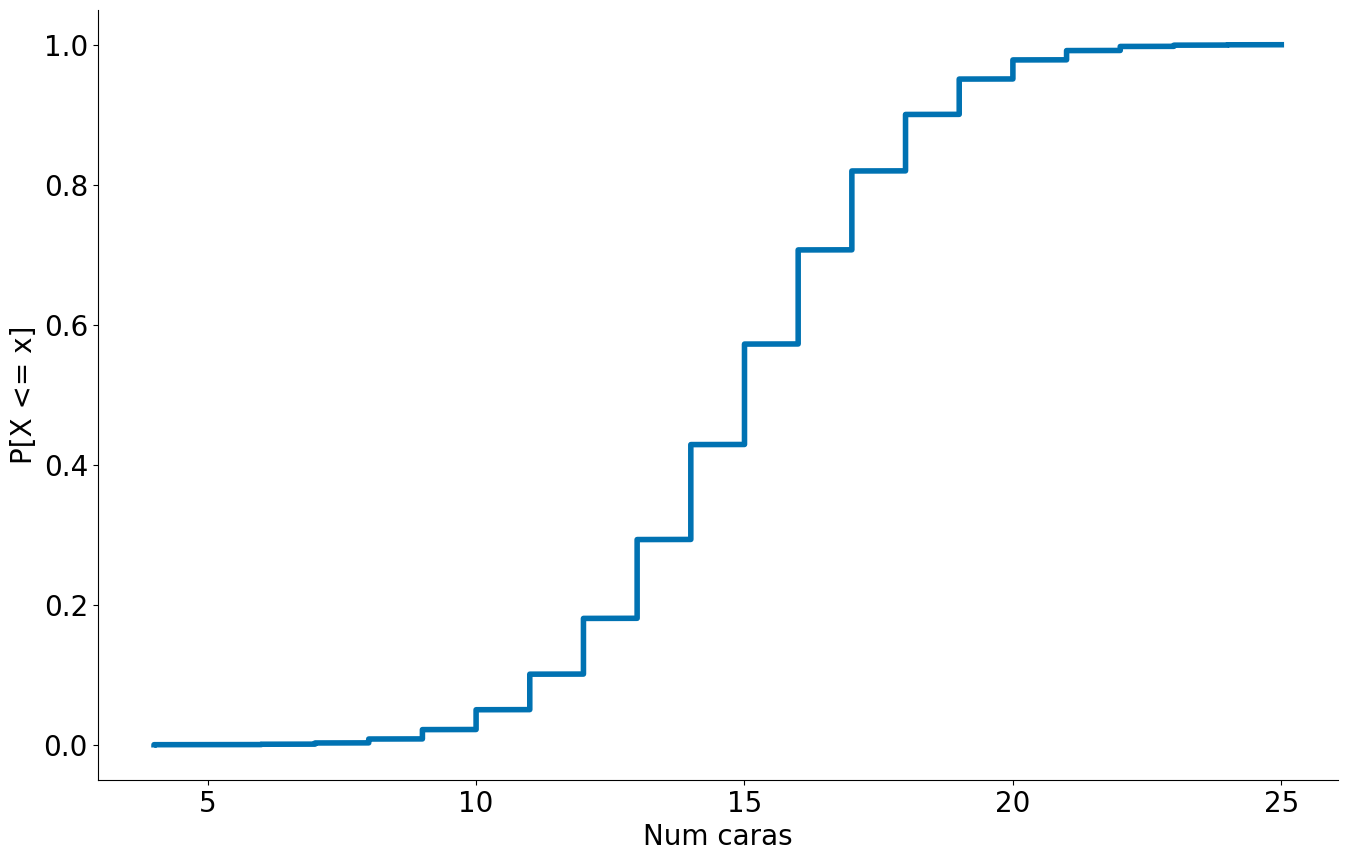
#In:
np.percentile(resultados, 2.5)
10.0
#In:
np.percentile(resultados, 97.5)
20.0
#In:
ecdf(10)
0.02159
#In:
ecdf(21)
0.97828
Até agora eu estou assumindo muito.
- Sei da população
- Sei amostrar de forma uniforme da população.
E quando eu estiver apenas com 1 amostra?!
- amostras = []
- para cada amostra de tamanho 100:
- amostra[i] = np.mean(amostra)
- plt.hist(amostras) –> normal
- estou trabalhando com uma delas: amostra[10]
Quando não sabemos de muita coisa
Preste atenção a partir daqui
Não sei nem jogar uma moeda para cima. Desempilhe o TCL.
Lembre-se que distribuição Binomial captura a média de caras esperadas em n lançamentos. Note que, ao somar cada um dos meus experimentos estou justamente voltando para o TCL. A distribuição amostral aqui é a média de caras a cada 30 jogadas. Assim, podemos ver a aproximação abaixo.
#In:
bins = np.arange(0, 31) + 0.5
plt.hist(resultados, bins=bins, edgecolor='k', density=True);
plt.xlabel('Numero de Caras')
plt.ylabel('Fração de Casos')
x = np.linspace(0, 31, 1000)
y = ss.distributions.norm.pdf(loc=np.mean(resultados),
scale=np.std(resultados, ddof=1), ## ddof=1 faz dividir por n-1
x=x)
plt.plot(x, y, label='Aproximação Normal')
plt.legend()
despine()
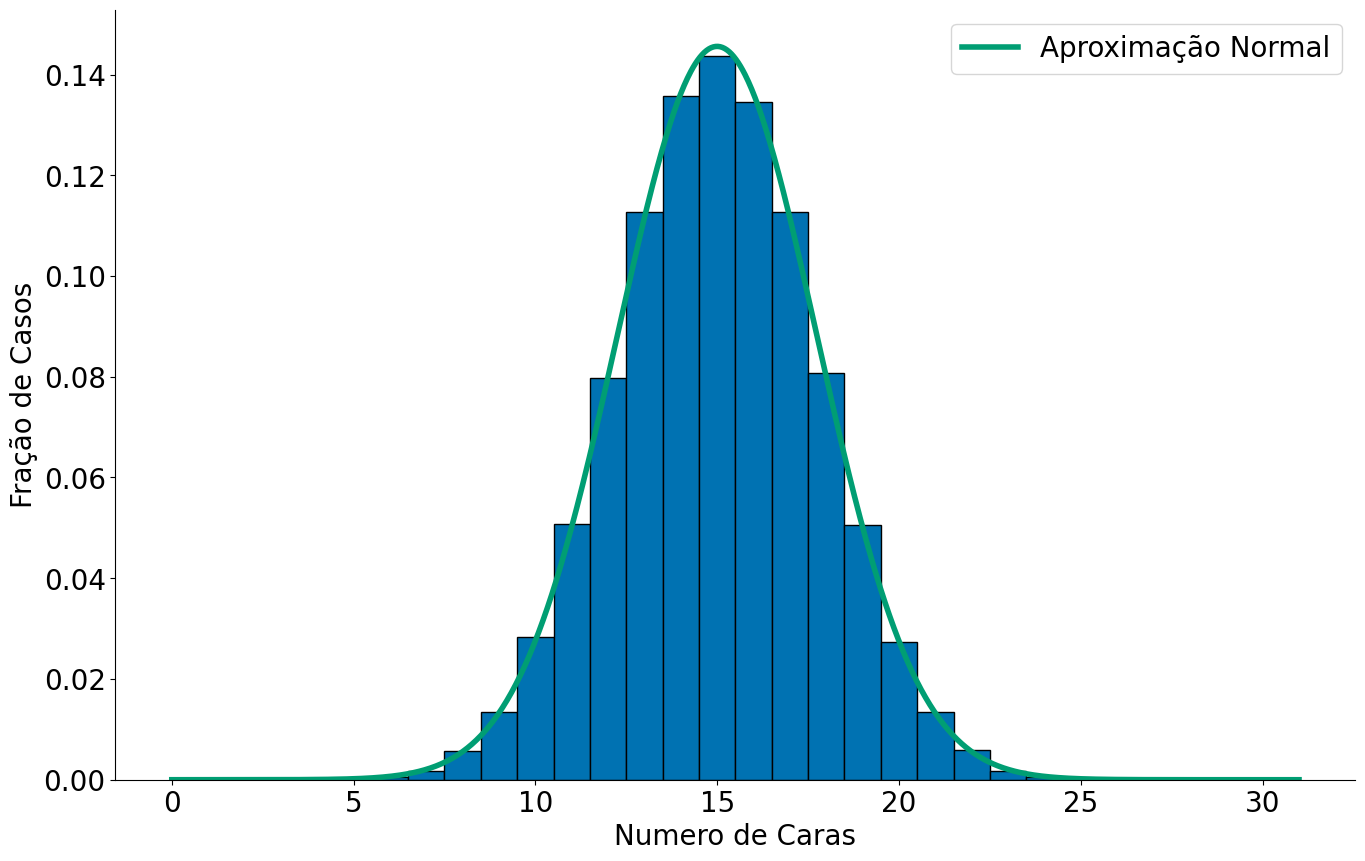
Qual o siginificado do plot acima??
- Cada experimento foi n-lançamentos. Tiramos a média dos n.
- Tenho a variância das médias, ou seja, a variância do estimaodor (lembre-se das aulas passadas)
- Resultado final –> Normal!
Observe como com uma única jogada de 30 moedas eu chego em uma normal bem próxima da anterior!
Cada jogo é um vetor de booleans.
#In:
np.random.randint(0, 2, size=30)
array([1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0,
1, 1, 0, 0, 1, 0, 1, 1])
A média é a fração de caras
#In:
np.random.randint(0, 2, size=30).mean()
0.6666666666666666
E ao multiplicar por 30, tenho o número de caras, afinal foram 30 lançamentos.
#In:
np.random.randint(0, 2, size=30).mean() * 30
13.0
Colando tudo junto, note que estou computando o desvio do estimador! Para isto, use a variância do estimador.
$Var(\hat{\mu}) = s^2 / n$
$Std(\hat{\mu}) = s / \sqrt{n}$
#In:
uma_vez = np.random.randint(0, 2, size=30)
mean_uma = np.mean(uma_vez) * 30
std_uma = np.std(uma_vez, ddof=1) * 30 # o desvio padrão é na mesma unidade da média
std_est = std_uma / np.sqrt(30)
Observe uma normal muito próxima da anterior com uma jogada!
#In:
x = np.linspace(0, 31, 1000)
y = ss.distributions.norm.pdf(loc=mean_uma,
scale=std_est,
x=x)
plt.plot(x, y, label='Aproximação Normal com Uma Amostra')
plt.legend()
despine()

Observe que ao fazer várias amostras existe uma variabilidade na normal estimada. Vamos entender teóricamente.
#In:
for _ in range(30):
uma_vez = np.random.randint(0, 2, size=30)
mean_uma = np.mean(uma_vez) * 30
std_uma = np.std(uma_vez, ddof=1) * 30
std_est = std_uma / np.sqrt(30)
x = np.linspace(0, 31, 1000)
y = ss.distributions.norm.pdf(loc=mean_uma,
scale=std_est,
x=x)
plt.plot(x, y)
despine()

ICs com Normal
Considere o caso que tenho UMA amostra apenas. Aqui eu não tenho mais distribuição amostral, pois só fiz uma coleta de dados. Felizmente, eu tenho algo para me ajudar, o TCL.
Quando o TCL funciona, podemos computar o intervalo de confiança usando uma Normal. Essa é a base comum que motivamos algumas aulas atrás. Vamos brincar um pouco de shiftar/escalar nossa Normal. Sabendo que:
\[\frac{1}{n}(X_1 + \cdots + X_n) \sim Normal(\mu, \sigma/\sqrt{n}).\]Vamos fazer:
\[Z_i = X_i - \mu\]Note que estamos apenas jogando todo mundo para a esquerda $-\mu$. O valor esperado (média) de uma VA X, $E[x]$, menos uma constante $c$ nada mais é do que $E[x]-c$. Além do mais, a variânçia não muda. Veja as propriedades no Wikipedia.
Assim:
\[\frac{1}{n}\sum_i Z_i = \frac{1}{n}\sum_i X_i - \mu \sim Normal(0, \sigma/\sqrt{n})\]Agora, vamos dividir $Z_i$ por. Neste caso, o desvio padrão e a média vão ser divididos pelo mesmo valor:
\[\frac{1}{n}\sum_i Z_i = \frac{1}{n}\sum_i \frac{X_i - \mu}{\sigma/\sqrt{n}} \sim Normal(0, 1)\]Isto quer dizer que a média (note a soma e divisão por n) das distribuições amostrais $Z_i$ seguem uma $Normal(0, 1)$. Note que estamos assumindo que o TCL está em voga. Às vezes (quando quebramos IID ou Variância finita), o mesmo não vale, mas vamos ignorar tais casos. Bacana, e daí? Não importa a população inicial, essa é a beleza do TCL!.
Então, mesmo sem saber a média real da população $\mu$, eu posso brincar com a equação acima. Primeiramente vamos focar na média $\frac{1}{n}\sum_i Z_i$, vamos chamar esta distribuição de $Z$ apenas. Sabendo que uma população segue uma Normal, eu consigo facilmente saber onde caem 95\% dos casos. Isto é similar ao exemplo das moedas e da Binomial acima. Porém, note que eu não assumo nada da população dos dados.
Uma forma comum de computar tais intervalos é usando tabelas ou uma figura como a apresentada abaixo. Hoje em dia, podemos usar a função ppf. A mesma indica que 95% dos casos estão ente $-1.96$ e $1.96$.

#In:
ss.norm.ppf(0.975)
1.959963984540054
#In:
ss.norm.ppf(1-0.975)
-1.959963984540054
Agora eu preciso apenas voltar para $X$. Para tal, vamos fazer uso de estimador não viésado de $\sigma$, o desvio padrão da amostra.
\[s = \sqrt{\frac{\sum_i ({x_i - \bar{x}})^2}{n-1}}\]Fazendo $z=1.96$ e $P(-z \le Z \le z) = 0.95$
\begin{align} 0.95 & = P(-z \le Z \le z)=P \left(-1.96 \le \frac {\bar X-\mu}{\sigma/\sqrt{n}} \le 1.96 \right)
& = P \left( \bar X - 1.96 \frac \sigma {\sqrt{n}} \le \mu \le \bar X + 1.96 \frac \sigma {\sqrt{n}}\right). \end{align}
Substituindo $\sigma$ por $s$: a probabilidade da média da população está entre $\bar{X} +- 1.96 \frac \sigma {\sqrt{n}}$ é de 95%.
- https://en.wikipedia.org/wiki/Variance#Properties
- https://en.wikipedia.org/wiki/Expected_value#Basic_properties
Computando um IC dos dados
#In:
# brinque com este valor um pouco, observe a mudança nas células abaixo.
TAMANHO_AMOSTRA = 100
resultados = []
for i in range(TAMANHO_AMOSTRA):
jogadas = np.random.randint(0, 2, size=30) # joga 30 moedas para cima
n_caras = (jogadas == 1).sum() # conta quantas foram == 1, caras
resultados.append(n_caras)
#In:
s = np.std(resultados, ddof=1)
s
2.8306404315146163
#In:
s_over_n = s / np.sqrt(len(resultados))
s_over_n
0.2830640431514616
#In:
mean = np.mean(resultados)
mean
15.26
#In:
mean - 1.96 * s_over_n
14.705194475423134
#In:
mean + 1.96 * s_over_n
15.814805524576865
#In:
# até aqui.
Entendendo um IC
Diferente de quando temos uma distribuição populacional, temos que interpretar o IC diferente. Note que:
- Não estamos computando onde caem 95% dos casos da população. Basta comparar os valores acima.
- Não estamos computando onde caem 95% das médias. Bast comparar com os valores acima.
Estamos resolvendo:
\[P(-z \le Z \le z)=P \left(-1.96 \le \frac {\bar X-\mu}{\sigma/\sqrt{n}} \le 1.96 \right)\]E chegando em:
\[P \left( \bar X - 1.96 \frac \sigma {\sqrt{n}} \le \mu \le \bar X + 1.96 \frac \sigma {\sqrt{n}}\right)\]EU TENHO 95% DE CONFIANÇA DE QUE A MÉDIA ESTÁ ENTRE $X +- 1.96 \frac \sigma {\sqrt{n}}$
#In:
# Construindo um IC
(mean - 1.96 * s_over_n, mean + 1.96 * s_over_n)
(14.705194475423134, 15.814805524576865)
95% de chance da média cair no intervalo de tamanho n acima. O mesmo não inclui o 22, então podemos assumir que o valor é não esperado.
Observe que existe uma chance de cometermos erros, qual é?
A situação mais comum na vida real
Normalmente temos uma amostra da população apenas. Daí não conhecemos a distribuição amostral. Mas gostaríamos de a partir da nossa amostra estimar onde está a estatística para a população.
Exemplo: queremos estimar qual a proporção de pessoas que gostará do produto (a estatística) entre todos os usuários (a população) a partir do cálculo da proporção de pessoas que gostou do produto (a mesma estatística) em um teste com 100 pessoas (a amostra).
Repare que se conhecermos como a estatística varia na distribuição amostral (ex: 2 pontos pra mais ou pra menos cobrem 99% dos casos) e temos a estatística calculada para a amostra, poderíamos estimar uma faixa de valores onde achamos que a estatística está para a população com 99% de confiança.
A ideia central que usaremos
Para exemplificar o caso acima, vamos explorar alguns dados reais de salários da Billboard. A ideia principal que usaremos, em uma técnica chamada boostrapping é que usar a amostra como substituto da população e simular a amostragem através de reamostragem com reposição fornece uma estimativa precisa da variação na distribuição amostral.
Para implementar o Bootstrap, vamos implementar uma função para o bootstrap_raw. A mesma faz uso da função df.sample que gera uma amostra aleatória de n elementos retirados do df. O funcionamento é similar a função np.random.choice. Note que estamos fazendo um bootstrap da mediana, podemos fazer patra outras medidas centrais.
- Dado
nesize - Gere
namostras de tamanhosizecom reposição - Tira a mediana (podia ser média ou qualquer outra medida central)
- Retorne as novas amostras e veja a distribuição das mesmas
#In:
def bootstrap_median(df, col, n=5000, size=None):
if size is None:
size = len(df)
values = np.zeros(n)
for i in range(n):
sample = df.sample(size, replace=True)
values[i] = sample[col].median()
return values
#In:
# 1. lendo dados
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/09-ICs/billboard_2000_2018_spotify_lyrics.csv',
encoding='iso-8859-1', na_values='unknown')
# 2. removendo na
df = df.dropna()
df = df[['title', 'main_artist', 'duration_ms']]
# 3. convertendo para minutos
df['duration_m'] = df['duration_ms'] / (60*1000)
# 4. apagando coluna antiga
del df['duration_ms']
df.head(5)
| title | main_artist | duration_m | |
|---|---|---|---|
| 1017 | Unsteady | x ambassadors | 3.225767 |
| 1018 | Too Much Sauce | dj esco | 3.718217 |
| 1021 | Key To The Streets | yfn lucci | 4.699783 |
| 1024 | Careless Whisper | wham! | 5.205917 |
| 1025 | Faith | george michael | 3.220000 |
Imagine por agora que os dados que temos de apenas 100 música Billboard são completos. Sei que tenho mais no df, mas preciso de small data aqui para executar o notebook.
#In:
df = df.sample(100)
#In:
plt.hist(df['duration_m'], bins=30, edgecolor='k')
plt.xlabel('Duração em minutos')
plt.ylabel('P[mediana]')
despine()

A mediana foi de:
#In:
df['duration_m'].median()
3.7401083333333336
Se calcularmos a mediana do números de novas músicas para três amostras de 1000 elementos, teremos 3 resultados diferentes. Estamos usando 1000 pois é o mesmo tamanho da nossa falsa população. A ideia do bootstrap é usar amostras da amostra original como diferentes visões da população.
#In:
for _ in range(3):
print(df['duration_m'].sample(len(df), replace=True).median())
print()
3.7260833333333334
3.7479
3.7006666666666668
Se fizermos isso muitas vezes podemos ver como essa variação acontece. Em particular, vamos fazer 10000 vezes. Note que o código abaixo é essenciamente o mesmo da função bootstrap acima.
#In:
S = len(df)
N = 5000
values = np.zeros(N)
for i in range(N):
sample = df.sample(S, replace=True)
values[i] = sample['duration_m'].median()
print(values)
[3.66665833 3.73621667 3.76645 ... 3.72608333 3.796 3.80666667]
#In:
plt.hist(values, bins=30, edgecolor='k')
plt.xlabel('Mediana da Amostra de Tamanho 1000')
plt.ylabel('P(mediana)')
despine()

Usando a função score at percentile sabemos onde ficam 95% dos dados sintéticos.
#In:
np.percentile(values, 2.5)
3.6464499999999997
#In:
np.percentile(values, 97.5)
3.8417858333333332
Acamos de construir um IC.
Pegando por partes:
- Consideramos a amostra $A$ que tem tamanho $n$ como sendo um substituto da população
- Repetimos $b$ vezes o seguinte processo: criamos uma amostra de tamanho proporcional a $n$ obtendo elementos aleatoriamente de $A$, repondo cada elemento depois de cada sorteio.
- Calculamos a estatística $e$ que nos interessa (média, mediana, desvio padrão, o que for) para cada uma das $b$ amostras.
Como resultado, sabemos como a estatística $e$ varia em uma simulação de $b$ amostragens. Podemos usar os percentis para criar um IC. Assim, se estimamos que em $P[E <= e_l] = 0.025$ e $P[E > e_h] = 0.025$ ou $P[E <= e_h] = 0.975$, nosso IC será: $(e - e_l, e + e_h)$.
- Podemos usar bootstrap para tendências centrais não extremas.
- O bootstrap falha quando os dados tem cauda pesada.
Um pouco de código de animações abaixo, pode ignorar o mesmo!
Ingore daqui, caso queira
#In:
def update_hist(num, data):
plt.cla()
plt.hist(data[0:100 * (num+1)], bins=20, edgecolor='k')
plt.xlabel('Mediana da Amostra de Tamanho 1000')
plt.ylabel('P(mediana)')
despine()
#In:
values = bootstrap_median(df, 'duration_m')
fig = plt.figure()
ani = animation.FuncAnimation(fig, update_hist, 30, fargs=(values, ))
HTML(ani.to_html5_video())

Até aqui!
Brincando com o bootstrap
E se a amostra fosse muito menor? Parece que temos alguns problemas! Voltamos a estimar o histograma, qual o motivo?
#In:
S = 2
N = 5000
values = bootstrap_median(df, 'duration_m', size=S, n=N)
plt.hist(values, bins=20, edgecolor='k');
plt.xlabel('Mediana da Amostra de Tamanho 2')
plt.ylabel('P(mediana)')
despine()
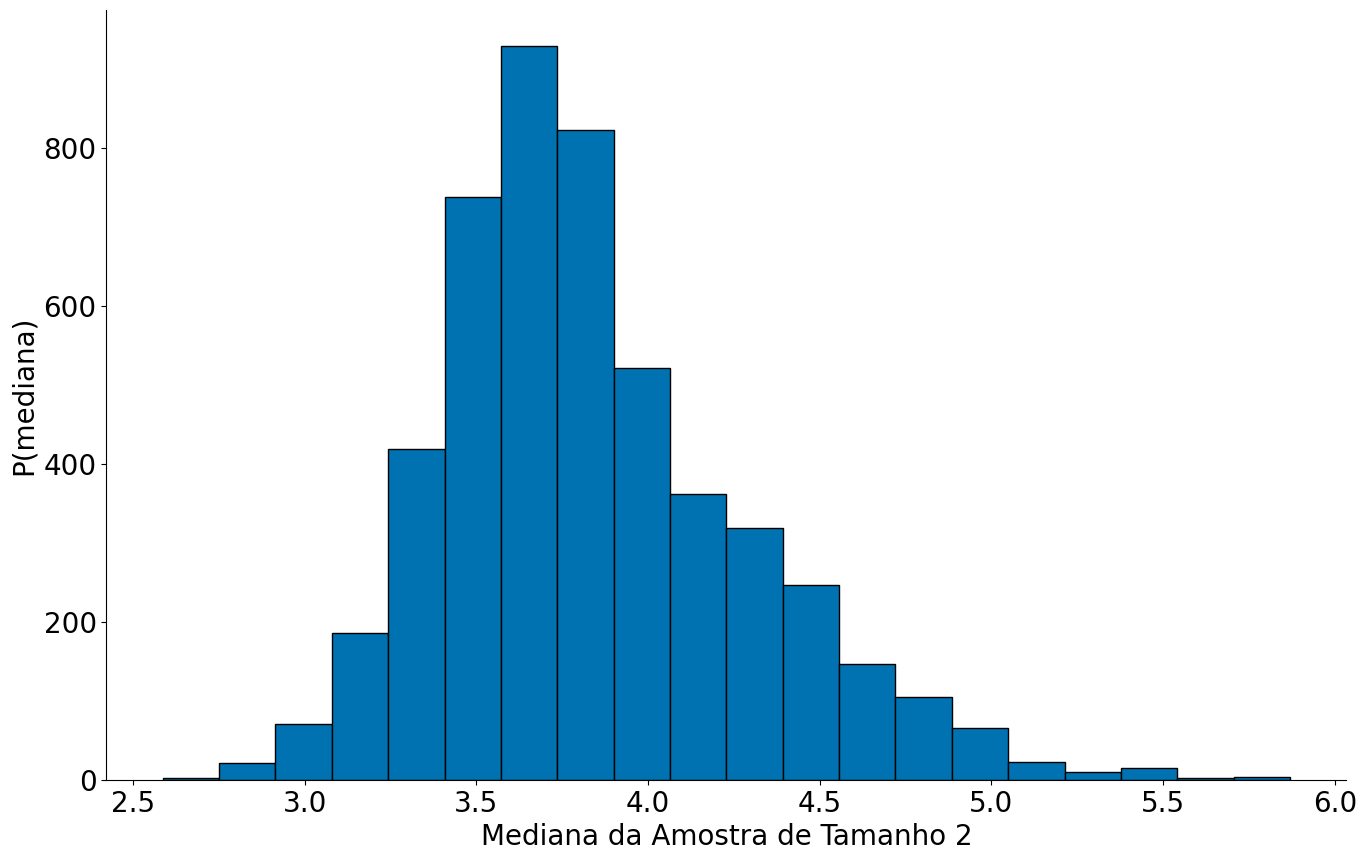
No geral, devemos gerar amostras perto do tamanho da amostra original, ou pelo menos algum valor alto. Note que algumas centenas, neste caso, já se comporta similar ao caso com 1000.
#In:
S = 30
N = 5000
values = bootstrap_median(df, 'duration_m', size=S, n=N)
plt.hist(values, bins=20, edgecolor='k');
plt.xlabel('Mediana da Amostra de Tamanho 30')
plt.ylabel('P(mediana)')
despine()
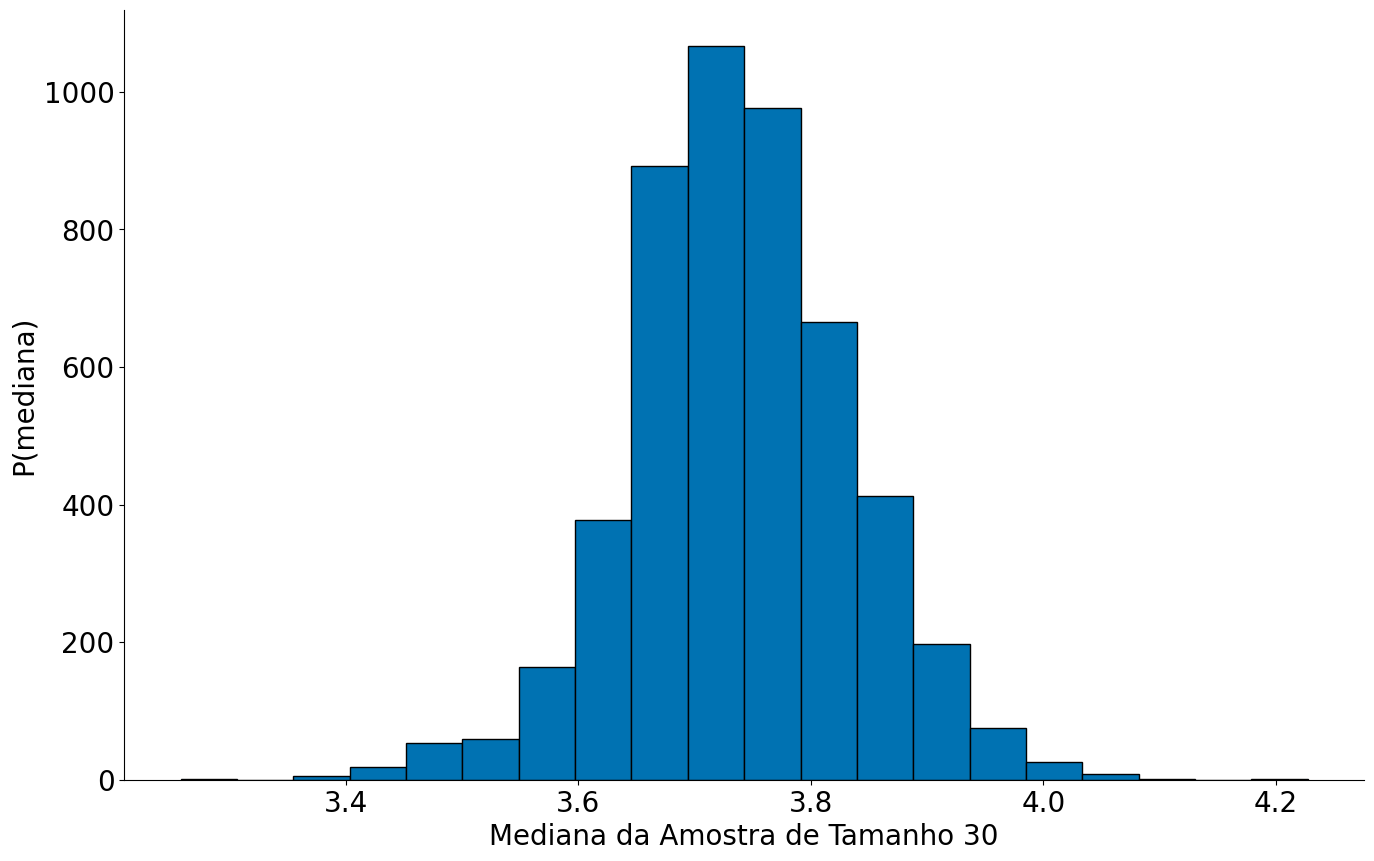
Um novo problema. Se forem poucas amostras, mesmo sendo um S razoável?!
#In:
S = len(df)
N = 10
values = bootstrap_median(df, 'duration_m', size=S, n=N)
plt.hist(values, bins=10, edgecolor='k');
plt.xlabel('Mediana de 10 amstras de Tamanho 100')
plt.ylabel('P(mediana)')
despine()
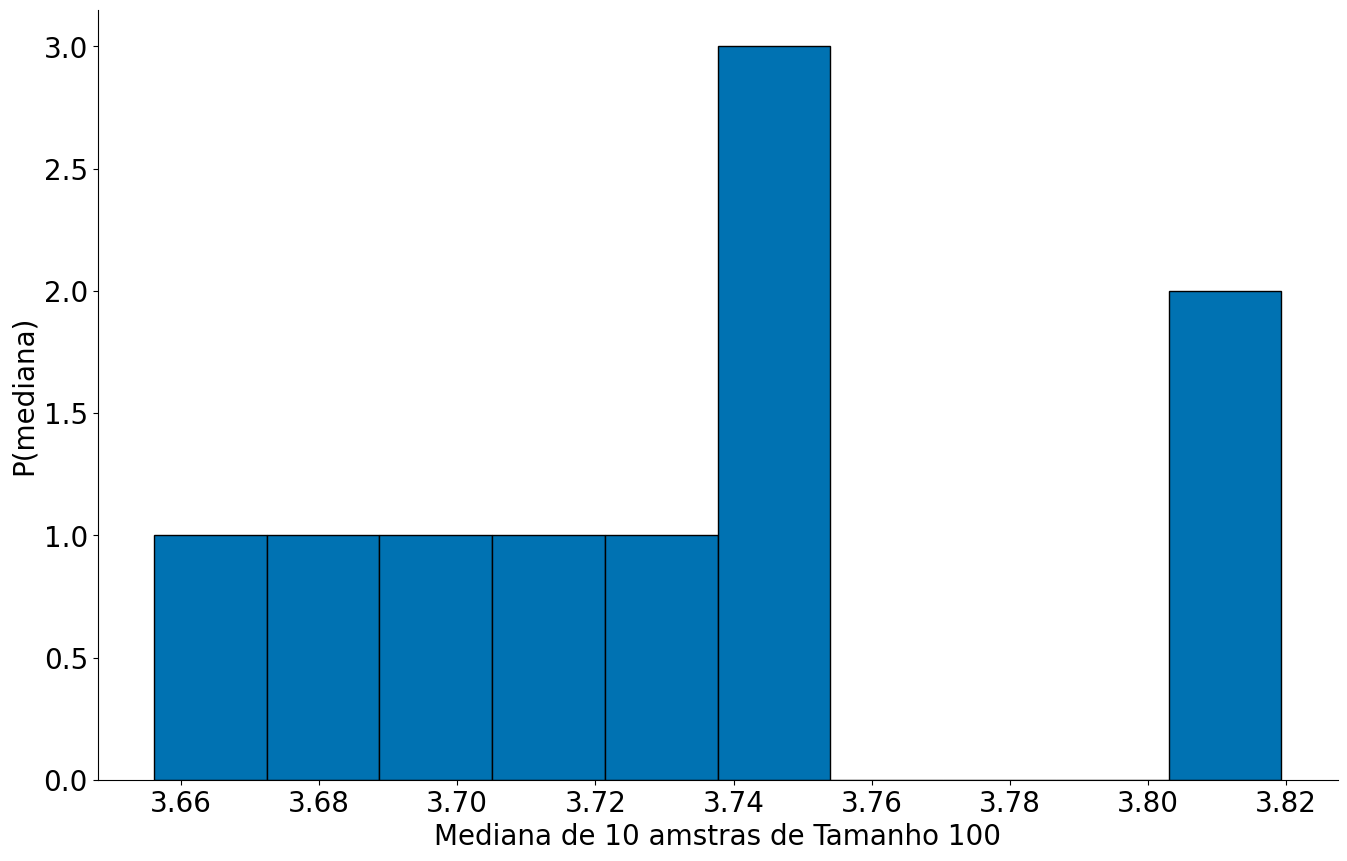
Gerando 2000 bootstraps e observar os que não capturam a mediana. O código abaixo demora usar um pouco de mágia numpy para executar de forma rápida.
Comparando o Bootstrap com o caso Teórico
#In:
# voltando para as moedas
TAMANHO_AMOSTRA = 100
resultados = []
for i in range(TAMANHO_AMOSTRA):
jogadas = np.random.randint(0, 2, size=30) # joga 30 moedas para cima
n_caras = (jogadas == 1).sum() # conta quantas foram == 1, caras
resultados.append(n_caras)
resultados = np.array(resultados)
#In:
def bootstrap_mean(x, n=5000, size=None):
if size is None:
size = len(x)
values = np.zeros(n)
for i in range(n):
sample = np.random.choice(x, size=size, replace=True)
values[i] = sample.mean()
return values
#In:
boot_samples = bootstrap_mean(resultados)
#In:
np.percentile(boot_samples, 2.5)
13.88
#In:
np.percentile(boot_samples, 97.5)
14.89
#In:
s = np.std(resultados, ddof=1)
s_over_n = s / np.sqrt(len(resultados))
mean = np.mean(resultados)
#In:
(mean - 1.96 * s_over_n, mean + 1.96 * s_over_n)
(13.887859806287713, 14.892140193712288)
#In:
plt.hist(boot_samples, edgecolor='k');

#In: