Amostragem
Amostrando sub-conjuntos de dados de forma inteligente.
Resultados Esperados
- Rever pequenos códigos de diferentes tipos de amostragem
- Entender amostragem uniforme e estratificada.
Sumário
#In:
# -*- coding: utf8
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
#In:
plt.ion()
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Durante a segunda parte do curso o uso de amostras vai ser aplicado para resolver problemas complexos. Embora se fala muito de big data, na prática, são boas amostras que são utilizadas para responder boas perguntas. Inclusive, existem falácias em big data quando a forma da amostra é muito viésada.
Vamos considerar uma base de dados de voos com atrasos nos estados unidos. Cada linha da tabela é composta de uma data, o número do vôo, destino e atraso do vôo em minutos.
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/08extra-Amostras/united_summer2015.csv')
df.head()
| Date | Flight Number | Destination | Delay | |
|---|---|---|---|---|
| 0 | 6/1/15 | 73 | HNL | 257 |
| 1 | 6/1/15 | 217 | EWR | 28 |
| 2 | 6/1/15 | 237 | STL | -3 |
| 3 | 6/1/15 | 250 | SAN | 0 |
| 4 | 6/1/15 | 267 | PHL | 64 |
Vamos assumir que esta é nossa população. Ou seja, eu estou apenas interessado em estudar dados de voos united do verão de 2015. Além do mais, a tabela representa um censo completo dos atrasos no ano.
A população consiste de quase 14 mil atrasos no ano de 2015.
#In:
df.shape
(13825, 4)
Vamos entender a distribuição dos atrasos:
#In:
delay_bins = np.append(np.arange(-20, 301, 10), 600)
plt.hist(df['Delay'], bins=delay_bins, edgecolor='k')
plt.xlabel('Atraso')
plt.ylabel('Número de Voos')
despine()
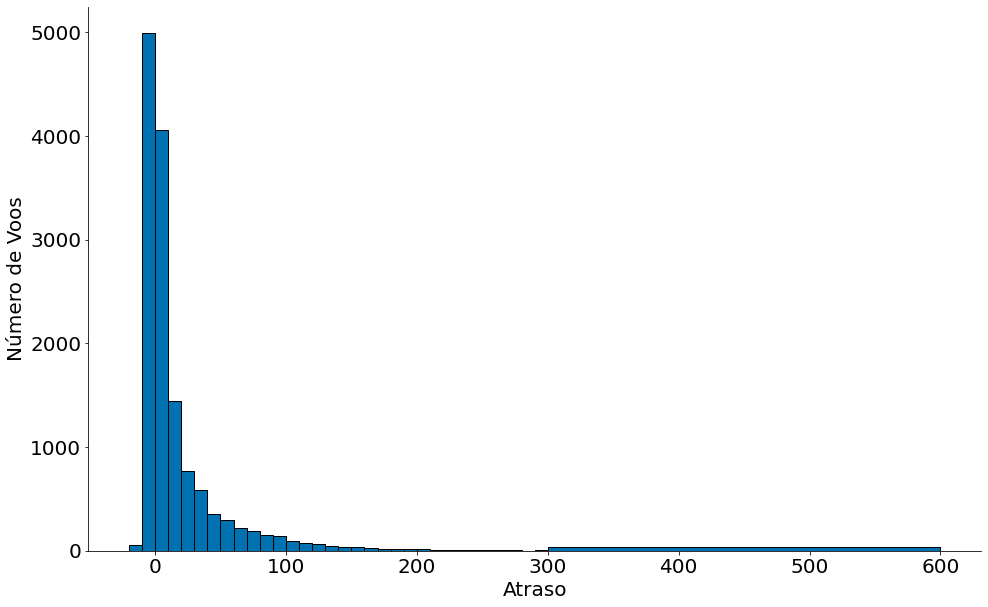
Agora vamos olhar para a mesmo distribuição quanto temos amostras menores dos nossos dados. Em particular, vamos iniciar com o caso de $n=1$. Note como a nova distribuição não parece com os dados da população.
#In:
def amostre_n(df, n):
index = df.index
novo = np.random.choice(index, size=n)
return df.loc[novo]
#In:
novo = amostre_n(df, 10)
plt.hist(novo['Delay'], bins=delay_bins, edgecolor='k')
plt.xlabel('Atraso')
plt.ylabel('Número de Voos')
despine()
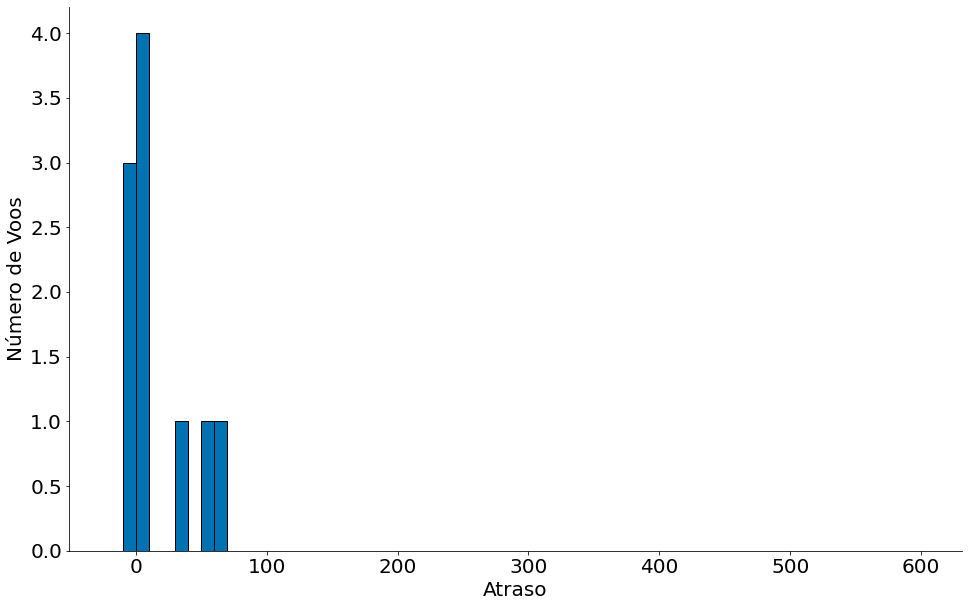
Na animação abaixo conseguimos ver o processo de chegar cada vez mais próximo da distribuição real. Portanto, cada frame da figura mostra o histograma com um valor de $n$ diferente. Quando $n$ se apróxima do valor da população, obviamente, vamos ter uma distribuição similar. Note que isto é uma forma de pensar na lei dos grandes números, ao aumentar $n$, aumentamos a chance de acertar cada bin do meu histograma. Lembre-se da simulação do dado.
#In:
from IPython.display import HTML
import matplotlib.animation
def animate(n):
novo = amostre_n(df, n)
plt.clf()
plt.title('N={}'.format(n))
plt.hist(novo['Delay'], bins=delay_bins, edgecolor='k')
plt.xlabel('Atraso')
plt.ylabel('Número de Voos')
despine()
fig = plt.figure()
n = np.arange(1, len(df), 200)
ani = matplotlib.animation.FuncAnimation(fig, animate, frames=n)
html = HTML(ani.to_html5_video())
html
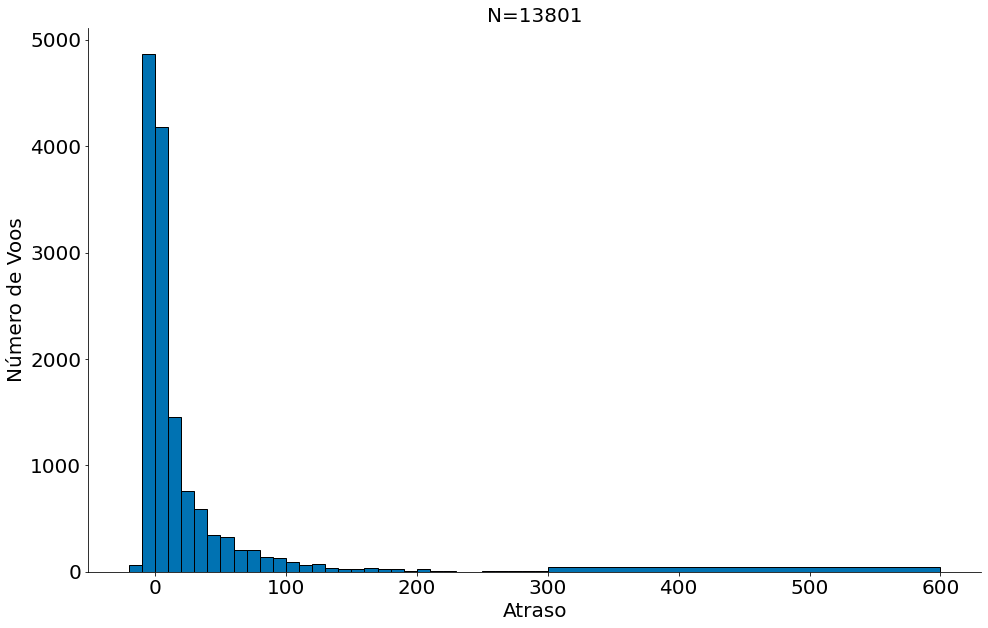
Problema de Poucas Amostras em uma Estatística
Note que com poucas amostras teremos problemas em computar a mediana. Por exemplo, abaixo eu escolho 100 voos e a mediana muda batante em cada rodada.
#In:
df['Delay'].median()
2.0
#In:
for _ in range(10):
novo = amostre_n(df, 1000)
print(novo['Delay'].median())
3.0
2.0
2.0
2.0
2.0
2.0
2.0
2.5
2.0
2.0
Além do mais, não podemos fazer nada se geramos amostras com algum viés. Por exemplo, se mensuramos atrasos em um único aeroporto!
#In:
for _ in range(10):
novo = amostre_n(df[df['Destination'] == 'ORD'], 100)
print(novo['Delay'].median())
6.5
3.0
2.5
5.0
2.5
5.0
4.0
0.5
3.0
3.0
Por fim, com uma amostragem estratificada, podemos garantir que temos uma proporção representativa de cada aeroporto.
#In:
novo = amostre_n(df, 100)
duas_colunas = novo[['Destination', 'Delay']]
print(duas_colunas.groupby('Destination').median())
Delay
Destination
ANC 11.5
AUS -7.0
BOS 2.5
CLE 104.0
DEN 13.0
EWR 3.0
HNL 3.0
IAD 2.0
IAH 18.5
JFK -1.0
KOA 4.0
LAS 14.0
LAX 25.5
LIH 1.0
MCO 16.0
OGG 0.0
ORD 8.0
PDX 6.0
PHL 5.0
PHX -2.0
PIT 47.0
RDU 12.0
SAN 15.5
SEA 9.0
SNA -2.0
#In:
from sklearn.model_selection import StratifiedShuffleSplit
for train, test in StratifiedShuffleSplit(test_size=200).split(df, df['Destination']):
duas_colunas = df[['Destination', 'Delay']]
amostra = duas_colunas.iloc[test]
print(amostra.groupby('Destination').median())
break
Delay
Destination
ANC -1.0
ATL -2.0
AUS -6.0
BOS 1.5
BWI 81.0
CLE -2.0
DCA 4.0
DEN 1.5
DFW -6.5
EWR 1.0
FLL 15.0
HNL 30.0
IAD -1.0
IAH 4.0
IND 9.0
JFK 0.0
KOA 7.0
LAS -0.5
LAX 7.0
LIH -1.0
MCO 7.5
MSP 57.0
OGG 4.0
ORD 4.0
PDX -2.0
PHL 2.0
PHX -2.5
PIT 6.0
RDU -3.0
RNO 2.0
SAN 2.5
SEA 0.0
SLC -5.0
SNA -3.0
STL -1.0
Qual o motivo de simular?
Para muitos casos, tipo a distribuição de médias, o teorema central do limite vai nos ajudar teoricamente pois sabemos que os dados da ditribuição de amostragem converge para uma normal. Note que isto não vai ser o caso para a mediana, porém podemos simular e ter uma ideia da mesma. Vamos iniciar olhando para a mediana.
Então muitos resultados teóricos podem ser feitos quando pensamos em distribuições amostrais da média, porém para a mediana simular é uma boa solução.
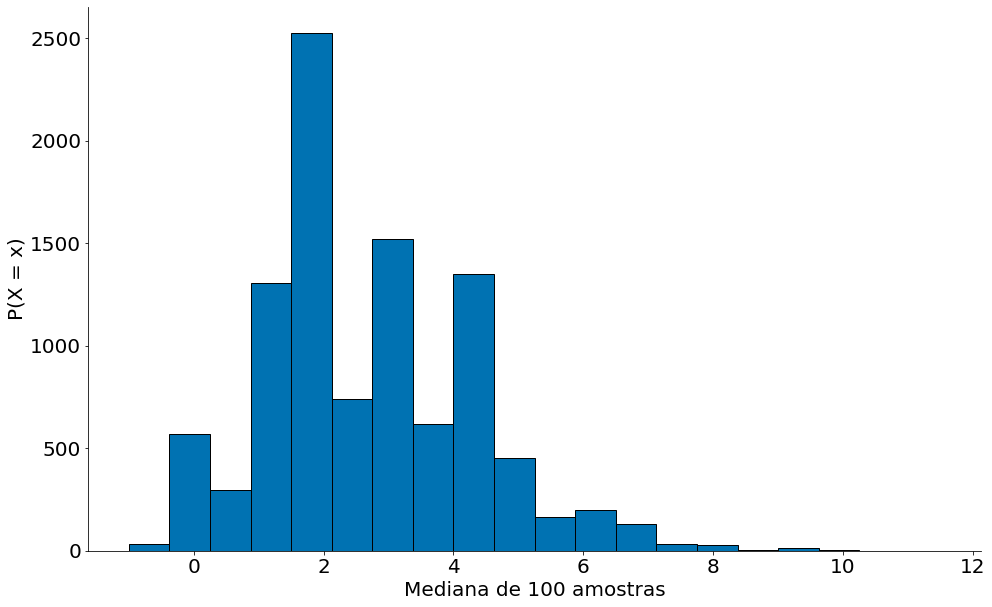
Abaixo brincamos um pouco com a distribuição amostral da mediana, note que a no fim não temos nada muito perto da normal.
#In:
amostral = []
for _ in range(10000):
novo = amostre_n(df, 100)
amostral.append(novo['Delay'].median())
#In:
plt.hist(amostral, bins=20, edgecolor='k');
plt.xlabel('Mediana de 100 amostras')
plt.ylabel('P(X = x)')
despine()