Teorema Central do Limite
O teorema base para os nossos testes de hipóteses
Resultados Esperados
- Revisar conceitos de Probabilidade ligados a distribuição normal
- Revisar o teorema central do limite
- Entendimento do teorema central do limite
- Simular médias de qualquer distribuição
- Mostrar como a distribuição de média segue uma normal
Sumário
#In:
# -*- coding: utf8
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#In:
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['axes.labelsize'] = 20
plt.rcParams['axes.titlesize'] = 20
plt.rcParams['legend.fontsize'] = 20
plt.rcParams['xtick.labelsize'] = 20
plt.rcParams['ytick.labelsize'] = 20
plt.rcParams['lines.linewidth'] = 4
#In:
plt.ion()
#In:
def despine(ax=None):
if ax is None:
ax = plt.gca()
# Hide the right and top spines
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Only show ticks on the left and bottom spines
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
Introdução
Uma razão pela qual a distribuição normal é tão útil é o teorema central do limite, que diz (em essência) que uma variável aleatória definida como a média (ou soma) de um grande número de variáveis aleatórias independentes e identicamente distribuídas é aproximadamente distribuída normalmente. Em outras palavras, a distribuição amostral de médias segue uma normal.
Em detalhes, se $X_1, …, X_n$ são variáveis aleatórias. Em particular, todas as VAs foram amostradas de uma mesma população com média $\mu$ (finita), desvio padrão $\sigma$ (finito). Além do mais, a geração de cada VA é independente da outra, sendo toas identicamente distribuídas. Quando $n$ é grande, então
\[\frac{1}{n}(X_1 + \cdots + X_n)\]é aproximadamente distribuído por uma Normal com média $\mu$ e desvio padrão $\sigma/\sqrt{n}$. De forma equivalente (mas muitas vezes mais útil),
\[Z = \frac{(X_1 + \cdots + X_n) - \mu }{\sigma / \sqrt{n}}\]é aproximadamente uma normal com média 0 e desvio padrão 1.
\[Z \sim Normal(0, 1).\]Como transformar VAs?
Lemebre-se da aula passada que sabemos estimar:
\[\bar{x} \approx \mu\]e
\[s^2 \approx \sigma\]Além do mais, sabemos que a variância do estimador da média é:
\[Var(\hat{\mu}) = \frac{\sigma^2}{n}\]Assim:
\begin{align} \bar{X} \sim Normal(\mu, \frac{\sigma^2}{n})
\bar{X}- \mu \sim Normal(0, \frac{\sigma^2}{n})
\frac{\bar{X}- \mu}{\sigma / \sqrt{n}} \sim Normal(0, 1)
\end{align}
Exemplo das Moedas
Considere o caso de uma moeda sendo jogada para cima. Agora, escolhe um número n (tamanho da amostra), e gere amostras da mesma. Ou seja, jogue uma moeda para cima n vezes. Por fim, some quantas vezes a moeda cai em cara (ou coroa). Isto é uma soma para uma amostra de tamanho n.
O processo de geração destes dados é bem capturado por uma distribuição Binomial. Variáveis aleatórias binomiais, que possuem dois parâmetros $n$ e $p$. A distribuição binomial é útil para contar o número de sucessos $n$ dada uma probabilidade $p$. Por exemplo, quantas vezes ($n$) uma moeda ($p$) gera um o valor cara. Formalmente, uma variável aleatória Binomial($n, p$) é simplesmente a soma de $n$ variáveis aleatórias independentes de Bernoulli($p$), cada uma delas igual a $1$ com probabilidade $p$ e $0$ com probabilidade $1 - p$.
Ao gerar um valor de uma Binomial estamos falando “Jogue uma moeda para cima n vezes e conte quantas caras!”. No caso abaixo, jogue uma moeda para cima 5 vezes e conte quantas caras!
#In:
num_caras = np.random.binomial(5, 0.5)
num_caras
2
Vamos repetir o processo várias! Jogue uma moeda para cima 5 vezes, pare, respire, depois jogue mais 5. Por aí vai. Note que temos a contagem para cada experimento de tamanho 5.
#In:
np.random.binomial(5, 0.5, size=10)
array([2, 2, 3, 3, 3, 3, 3, 1, 2, 2])
Agora, vamos ver o gráfico de tal experimento!
#In:
num_caras_a_cada_5 = np.random.binomial(5, 0.5, size=10000)
plt.hist(num_caras_a_cada_5, bins=[-0.5, 0.5, 1.5, 2.5, 3.5, 4.5, 5.5], edgecolor='k')
plt.xlabel('Jogadas de moedas')
plt.ylabel('Número de caras')
plt.title('1000 jogadas de moedas em grupos de 5')
despine()
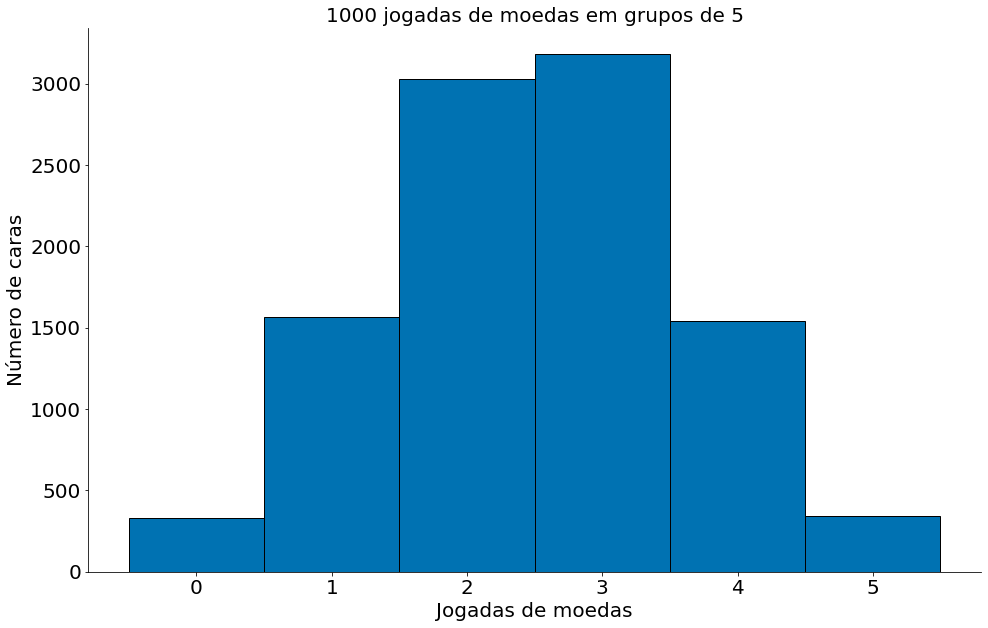
Mesma coisa com 10 moedas
#In:
num_caras_a_cada_5 = np.random.binomial(10, 0.5, size=1000000)
ticks = np.linspace(-0.5, 10.5, num=12)
print(ticks)
plt.hist(num_caras_a_cada_5, bins=ticks, edgecolor='k')
plt.xlabel('Jogadas de moedas')
plt.ylabel('Número de caras')
plt.title('1000 jogadas de moedas em grupos de 5')
despine()
[-0.5 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5]
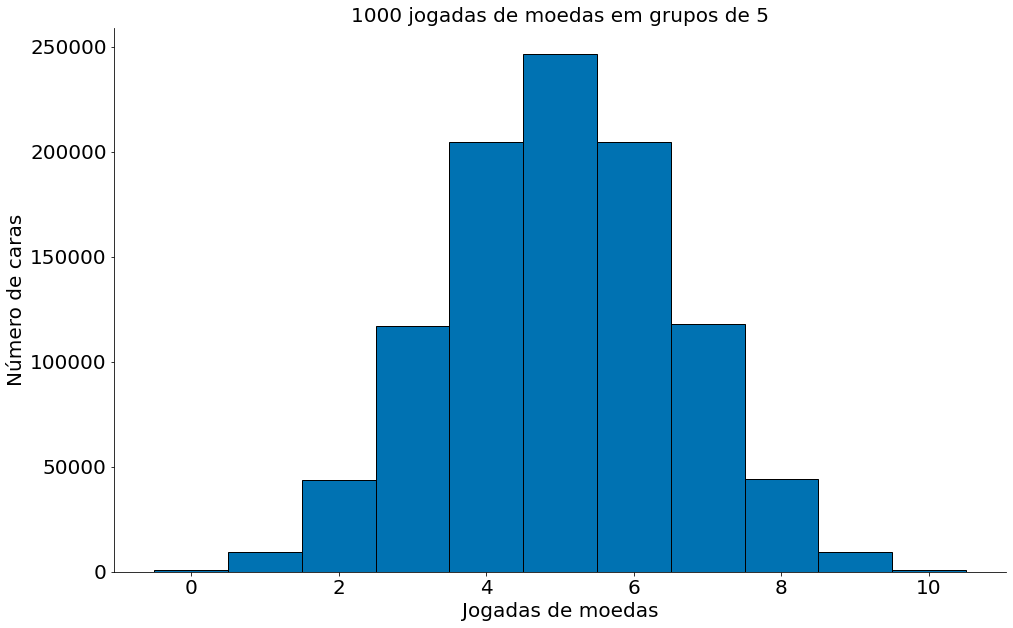
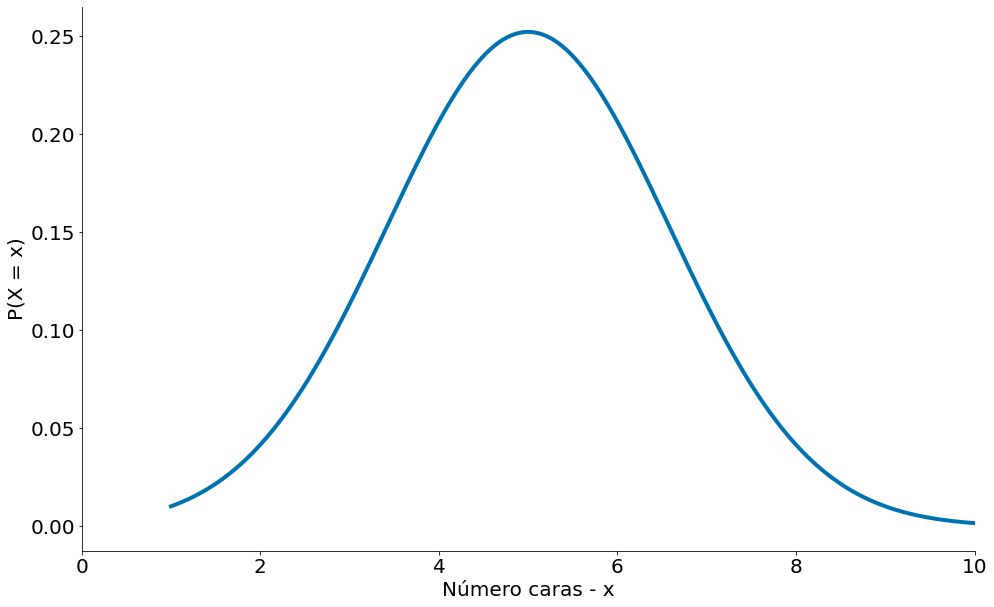
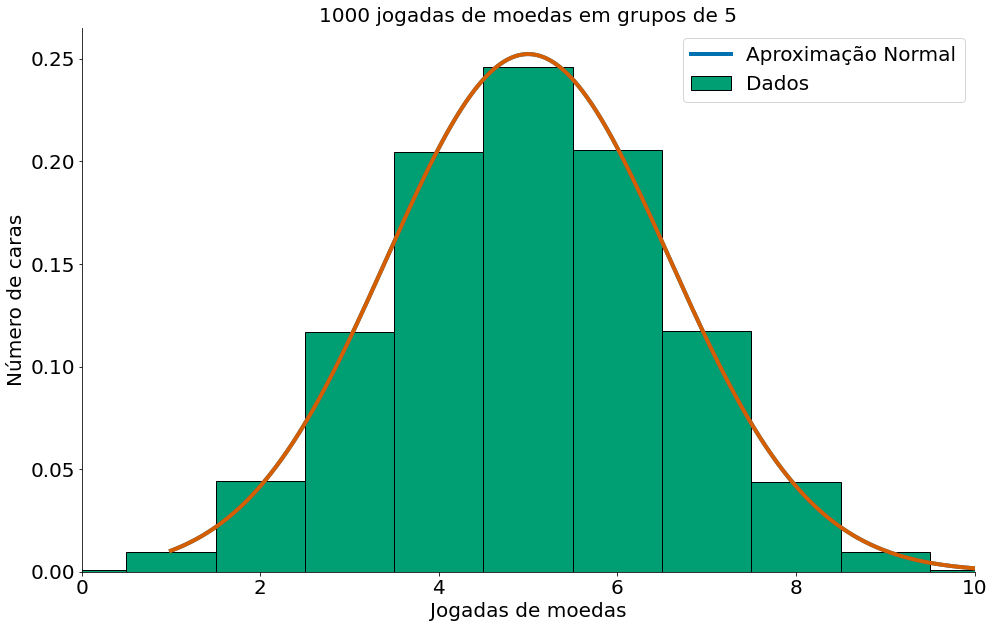
Lembrando da sua aula de probabilidade, uma população que segue uma variável Binomial($n, p$) tem média $\mu = np$ e desvio padrão $\sigma = \sqrt{np(1 - p)}$. Se plotarmos ambos, você pode facilmente ver a semelhança. Obseve o plot abaixo da PDF com os parâmetros que listamos (média, desvio padrão).
#In:
import scipy.stats as ss
mean = 10 * 0.5
std = np.sqrt(10 * 0.5 *(1 - 0.5))
x = np.linspace(1, 11, 1000)
y = ss.distributions.norm.pdf(loc=mean, scale=std, x=x)
plt.xlim(0, 10)
plt.plot(x, y)
plt.xlabel('Número caras - x')
plt.ylabel('P(X = x)')
despine()
#In:
mean = 10 * 0.5
std = np.sqrt(10 * 0.5 *(1 - 0.5))
x = np.linspace(1, 11, 1000)
y = ss.distributions.norm.pdf(loc=mean, scale=std, x=x)
plt.xlim(0, 10)
plt.plot(x, y, label='Aproximação Normal')
num_caras_a_cada_5 = np.random.binomial(10, 0.5, size=1000000)
ticks = np.linspace(-0.5, 10.5, num=12)
plt.hist(num_caras_a_cada_5, bins=ticks, edgecolor='k', label='Dados',
density=True)
plt.plot(x, y)
plt.xlabel('Jogadas de moedas')
plt.ylabel('Número de caras')
plt.title('1000 jogadas de moedas em grupos de 5')
plt.legend()
despine()
Exemplo com Dados Sintéticos de Matrículas
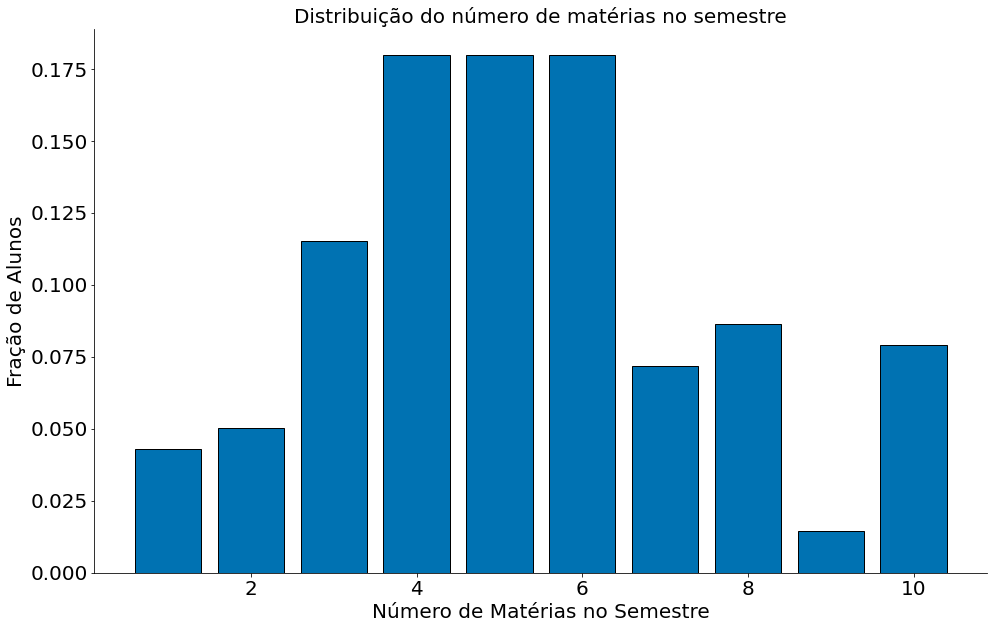
Para exemplificar com dados, considere o exemplo abaixo onde geramos uma distribuição sintética de 25 mil alunos da UFMG. A distribuição captura o número de matéria que um aluno se matrícula no ano. Note que diferente da moeda, que gera apenas cara ou cora, cada aluno pode se matricular entre [min, max] matérias. No exemplo, vamos suport que todo aluno precisa se matricular em pelo menos uma matéria min=1 e pode ser matricular em no máximo 10 matérias max=10. Agora, vamos suport que cada número de matéria tem probabilidade $p_i$. Ou seja, a chance se matricular em uma matéria é $p_1$ e por aí vai.
Dados deste tipo são modelados por distribuições multinomiais. Generalizando a Binomial, uma Multinomial conta a quantidade de sucessos (matrículas) em cada $p_i$. A mesma é definida por $n > 0$, número de amostras ou matrículas, e $p_1, \ldots, p_k$ probabilidade de se matrícular em $i$ matérias. A pmf de uma multinomial é dada por:
\[P(X = x) = \frac{n!}{x_1!\cdots x_k!} p_1^{x_1} \cdots p_k^{x_k}\]Inicialmente observe os valores de $p_i$.
#In:
num_materias = np.arange(10) + 1
prob_materias = np.array([6, 7, 16, 25, 25, 25, 10, 12, 2, 11])
prob_materias = prob_materias / prob_materias.sum()
plt.bar(num_materias, prob_materias, edgecolor='k')
plt.xlabel('Número de Matérias no Semestre')
plt.ylabel('Fração de Alunos')
plt.title('Distribuição do número de matérias no semestre')
despine()
Agora vamos responder a pergunta: Quantas matérias, em média, um aluno se matrícula?!. Note que a nossa pergunta aqui é em média!!. Então, vamos considerar que temos 25 mil discente na ufmg. Para cada um destes alunos, vamos amostrar de $p_i$ o número de matérias que tal aluno está matrículado no atual semestre.
#In:
amostras = 25000
mats = np.arange(10) + 1
print(mats)
dados = []
for i in range(25000):
n_mat = np.random.choice(mats, p=prob_materias)
dados.append(n_mat)
dados = np.array(dados)
dados
[ 1 2 3 4 5 6 7 8 9 10]
array([ 5, 10, 1, ..., 4, 7, 6])
Agora vamos responder nossa pergunta. Quantas matérias, em média, um aluno se matrícula?!. Para tirar uma média precisamos de uma amostra. Vamos definir amostras de tamanho 100. Então, vamos amostrar 100 alunos, com repetição, dos nossos 25 mil alunos.
#In:
n_amostra = 100
soma = 0
for i in range(n_amostra):
aluno = np.random.randint(0, len(dados))
num_mat = dados[aluno]
soma += num_mat
media = soma / n_amostra
print(media)
5.43
Vamos repetir o processo algumas vezes. Tipo, 10000 vezes.
#In:
n_amostra = 100
medias = []
for _ in range(10000):
soma = 0
for i in range(n_amostra):
aluno = np.random.randint(0, len(dados))
num_mat = dados[aluno]
soma += num_mat
media = soma / n_amostra
medias.append(media)
medias = np.array(medias)
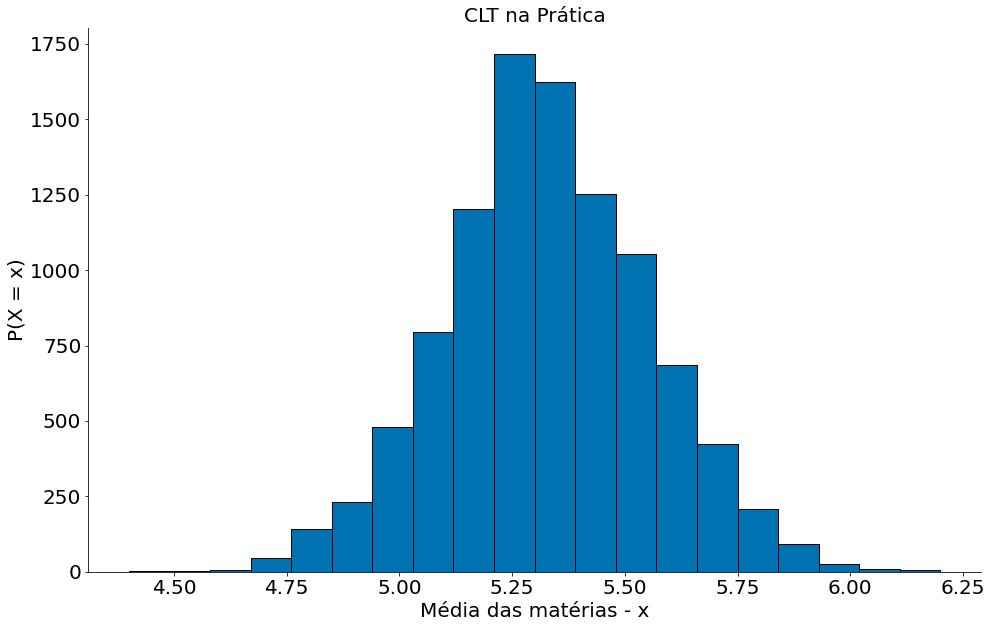
Agora vamos ver os resultados!
#In:
plt.hist(medias, bins=20, edgecolor='k')
plt.ylabel('P(X = x)')
plt.xlabel('Média das matérias - x')
plt.title('CLT na Prática')
despine()
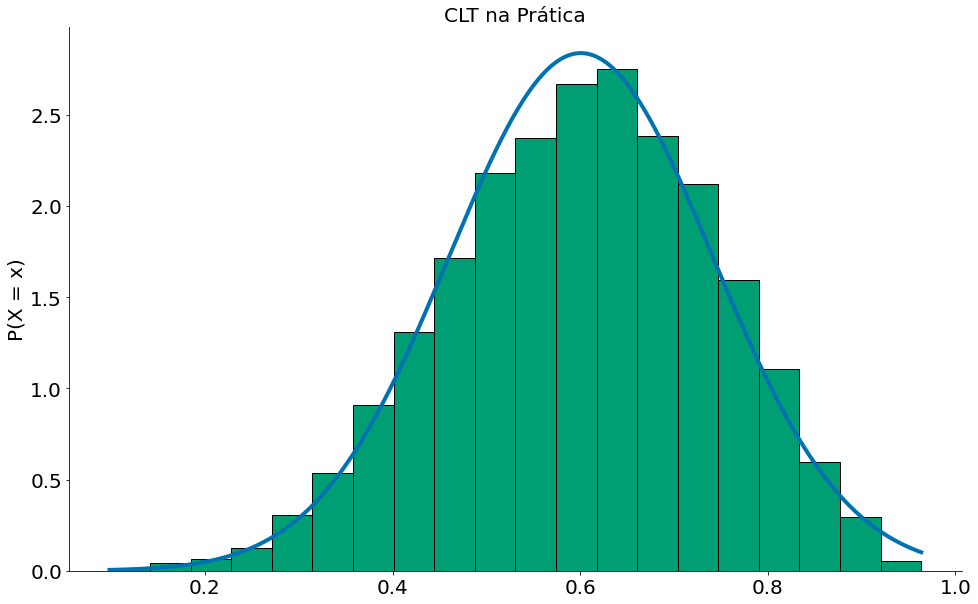
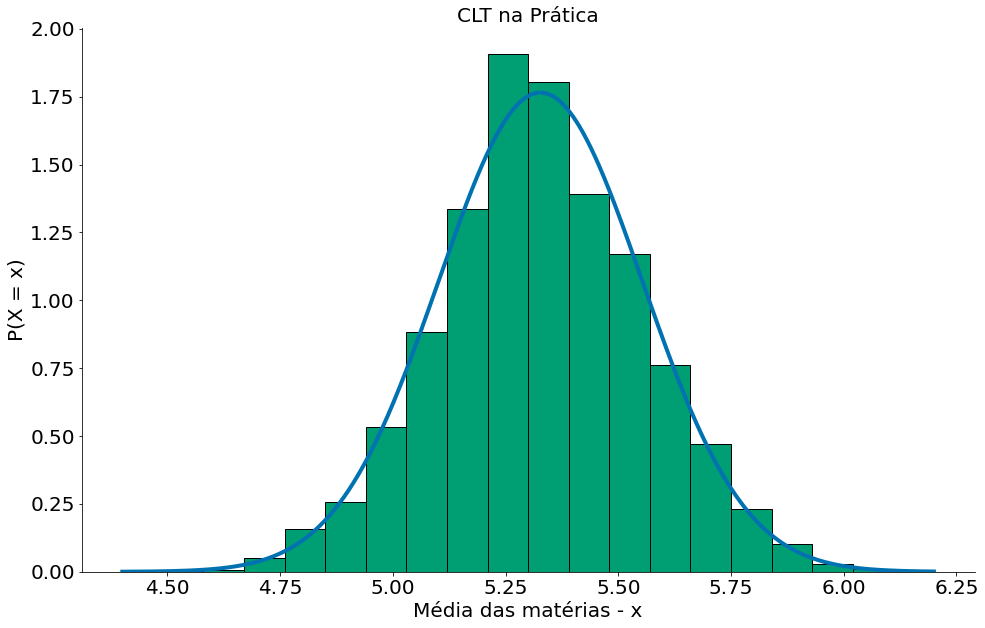
Agora, vamos comparar com a nossa Normal, para isto podemos usar a média das médias e o desvio padrão das médias.
#In:
mean = np.mean(medias)
# ddof=1 faz dividir por n-1
std = np.std(medias, ddof=1)
# pegue 1000 números entre o minimo e o max
x = np.linspace(np.min(medias), np.max(medias), 1000)
y = ss.distributions.norm.pdf(loc=mean, scale=std, x=x)
plt.plot(x, y, label='Aproximação Normal')
plt.hist(medias, bins=20, edgecolor='k', density=True)
plt.ylabel('P(X = x)')
plt.xlabel('Média das matérias - x')
plt.title('CLT na Prática')
despine()
Com Dados
#In:
df = pd.read_csv('https://media.githubusercontent.com/media/icd-ufmg/material/master/aulas/03-Tabelas-e-Tipos-de-Dados/nba_salaries.csv')
df.head()
| PLAYER | POSITION | TEAM | SALARY | |
|---|---|---|---|---|
| 0 | Paul Millsap | PF | Atlanta Hawks | 18.671659 |
| 1 | Al Horford | C | Atlanta Hawks | 12.000000 |
| 2 | Tiago Splitter | C | Atlanta Hawks | 9.756250 |
| 3 | Jeff Teague | PG | Atlanta Hawks | 8.000000 |
| 4 | Kyle Korver | SG | Atlanta Hawks | 5.746479 |
#In:
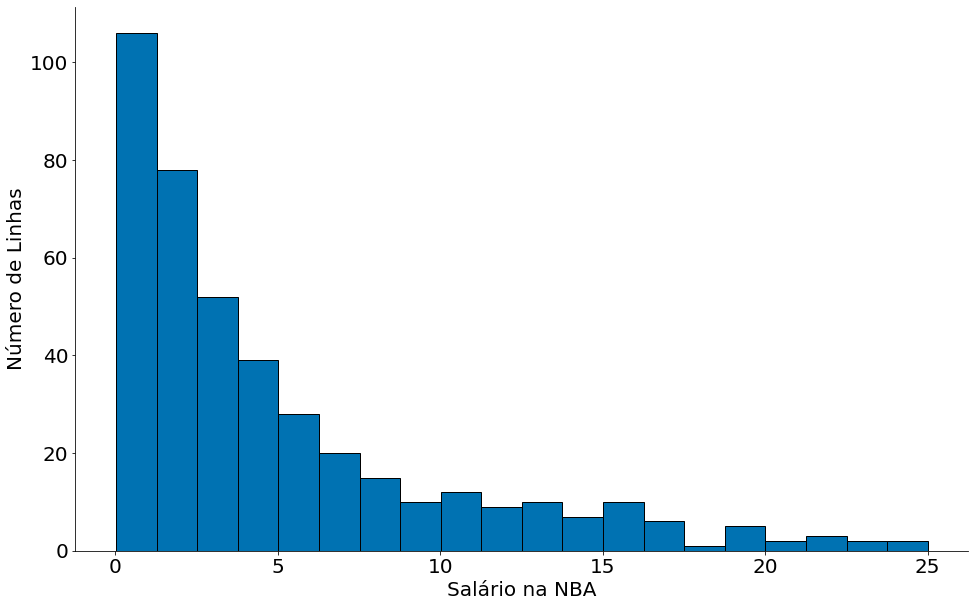
df['SALARY'].sort_values().plot.hist(bins=20, edgecolor='k')
plt.xlabel('Salário na NBA')
plt.ylabel('Número de Linhas')
despine()
#In:
N = 10000
data = df['SALARY']
medias = []
for i in range(N):
mean = np.random.choice(data, 100).mean()
medias.append(mean)
#In:
mean = np.mean(medias)
# ddof=1 faz dividir por n-1
std = np.std(medias, ddof=1)
# pegue 1000 números entre o minimo e o max
x = np.linspace(np.min(medias), np.max(medias), 1000)
y = ss.distributions.norm.pdf(loc=mean, scale=std, x=x)
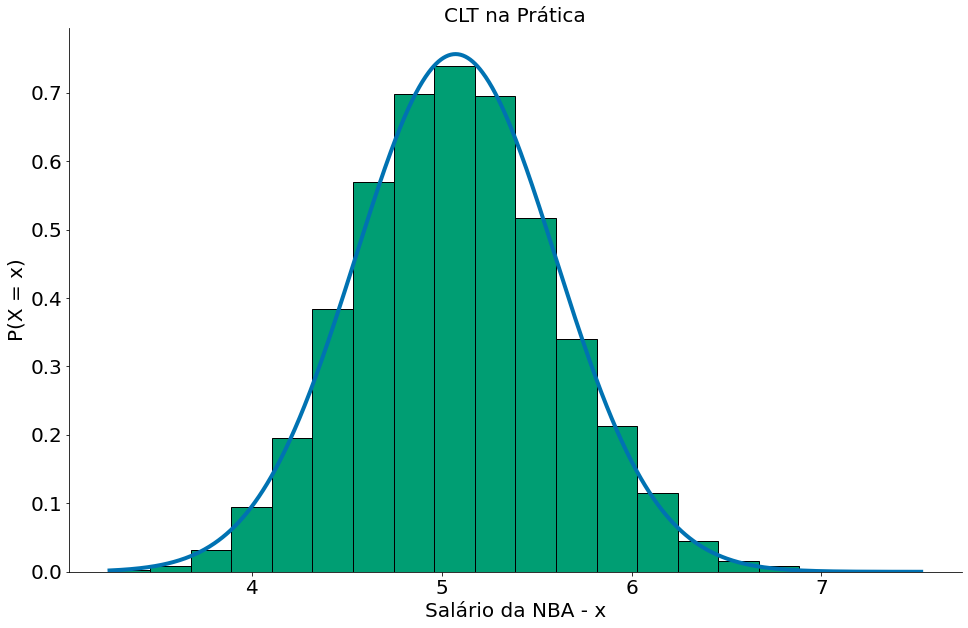
plt.plot(x, y, label='Aproximação Normal')
plt.hist(medias, bins=20, edgecolor='k', density=True)
plt.ylabel('P(X = x)')
plt.xlabel('Salário da NBA - x')
plt.title('CLT na Prática')
despine()
Condições para o TCL
Existem algumas condições para garantir que o TCL seja válido.
- Dados independentes e identicamente distribuídos.
- Variância finita.
- Pelo menos umas 30 amostras
Observe do wikipedia que uma distribuição Pareto(1) tem variância infinita. Quebramos nossa condição. Olhe que o plot abaixo não parece em nada com uma Normal.
https://en.wikipedia.org/wiki/Pareto_distribution
#In:
data = []
for _ in range(10000):
m = np.random.pareto(1, size=100).mean()
data.append(m)
#In:
plt.hist(data, bins=100, edgecolor='k')
despine()

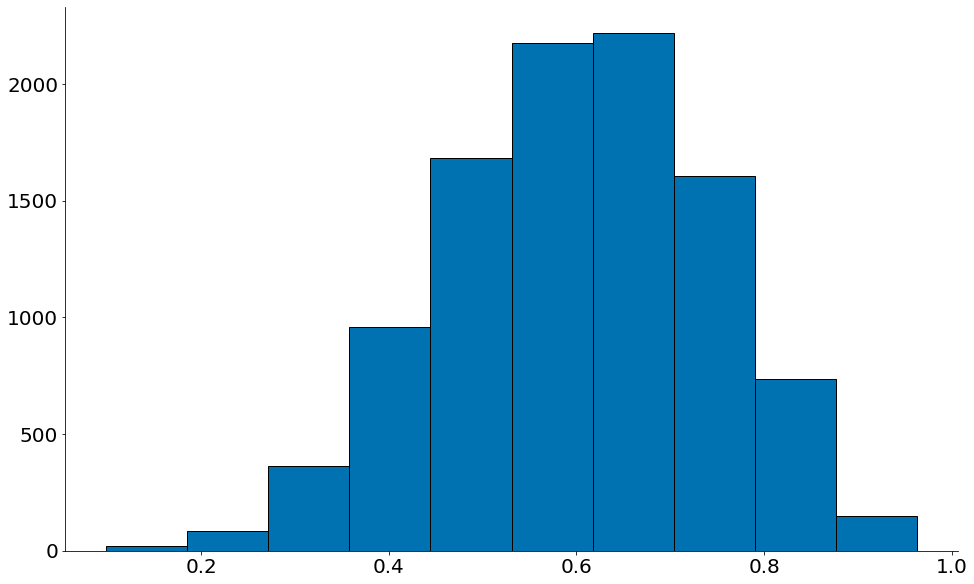
Podemos quebrar também com amostras muito pequenas, tipo na Beta(3, 2, size=2) abaixo.
Observe como é muito perto de uma Normal mas tem um certo viés para a direita.
#In:
data = []
for _ in range(10000):
m = np.random.beta(3, 2, size=2).mean()
data.append(m)
plt.hist(data, edgecolor='k')
despine()
#In:
mean = np.mean(data)
# ddof=1 faz dividir por n-1
std = np.std(data, ddof=1)
# pegue 1000 números entre o minimo e o max
x = np.linspace(np.min(data), np.max(data), 1000)
y = ss.distributions.norm.pdf(loc=mean, scale=std, x=x)
plt.plot(x, y, label='Aproximação Normal')
plt.hist(data, bins=20, edgecolor='k', density=True)
plt.ylabel('P(X = x)')
plt.title('CLT na Prática')
despine()